题目内容
已知圆C:x2+(y-3)2=4,一动直线l过A(-1,0)与圆C相交于P、Q两点,
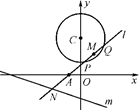
M是PQ中点,l与直线m:x+3y+6=0相交于N.
(1)求证:当l与m垂直时,l必过圆心C;
(2)当PQ=2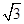 时,求直线l的方程;
时,求直线l的方程;
(3)探索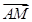 ·
· 是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.

M是PQ中点,l与直线m:x+3y+6=0相交于N.
(1)求证:当l与m垂直时,l必过圆心C;
(2)当PQ=2
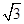 时,求直线l的方程;
时,求直线l的方程;(3)探索
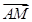 ·
· 是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.(1)见解析(2)x=-1或4x-3y+4=0.(3)-5
(1)证明:∵l与m垂直,且km=-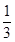 ,
,
∴kl=3.又kAC=3,所以当l与m垂直时,l的方程为y=3(x+1),l必过圆心C.
(2)解:①当直线l与x轴垂直时,易知x=-1符合题意.②当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),即kx-y+k=0.因为PQ=2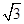 ,所以CM=
,所以CM=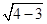 =1,则由CM=
=1,则由CM=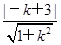 =1,得k=
=1,得k=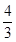 ,∴直线l:4x-3y+4=0.从而所求的直线l的方程为x=-1或4x-3y+4=0.
,∴直线l:4x-3y+4=0.从而所求的直线l的方程为x=-1或4x-3y+4=0.
(3)解:∵CM⊥MN,∴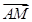 ·
· =(
=(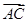 +
+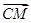 )·
)· =
=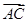 ·
· +
+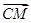 ·
· =
=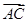 ·
· .
.
①当l与x轴垂直时,易得N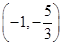 ,则
,则 =
=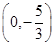 .又
.又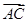 =(1,3),∴
=(1,3),∴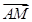 ·
· =
=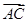 ·
· =-5;②当l的斜率存在时,设直线l的方程为y=k(x+1),则由
=-5;②当l的斜率存在时,设直线l的方程为y=k(x+1),则由
得N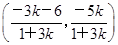 ,则
,则 =
=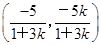 .
.
∴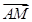 ·
· =
=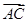 ·
· =
=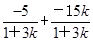 =-5.
=-5.
综上,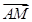 ·
· 与直线l的斜率无关,且
与直线l的斜率无关,且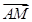 ·
· =-5.
=-5.
另解:连结CA并延长交m于点B,连结CM,CN,由题意知AC⊥m,又CM⊥l,∴四点M、C、N、B都在以CN为直径的圆上,由相交弦定理,得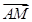 ·
· =-|AM|·|AN|=-|AC|·|AB|=-5.
=-|AM|·|AN|=-|AC|·|AB|=-5.
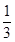 ,
,∴kl=3.又kAC=3,所以当l与m垂直时,l的方程为y=3(x+1),l必过圆心C.
(2)解:①当直线l与x轴垂直时,易知x=-1符合题意.②当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),即kx-y+k=0.因为PQ=2
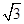 ,所以CM=
,所以CM=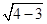 =1,则由CM=
=1,则由CM=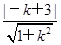 =1,得k=
=1,得k=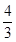 ,∴直线l:4x-3y+4=0.从而所求的直线l的方程为x=-1或4x-3y+4=0.
,∴直线l:4x-3y+4=0.从而所求的直线l的方程为x=-1或4x-3y+4=0.(3)解:∵CM⊥MN,∴
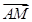 ·
· =(
=(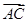 +
+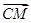 )·
)· =
=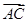 ·
· +
+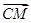 ·
· =
=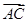 ·
· .
.①当l与x轴垂直时,易得N
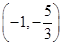 ,则
,则 =
=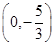 .又
.又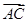 =(1,3),∴
=(1,3),∴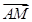 ·
· =
=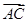 ·
· =-5;②当l的斜率存在时,设直线l的方程为y=k(x+1),则由
=-5;②当l的斜率存在时,设直线l的方程为y=k(x+1),则由
得N
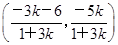 ,则
,则 =
=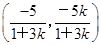 .
.∴
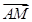 ·
· =
=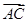 ·
· =
=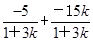 =-5.
=-5.综上,
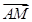 ·
· 与直线l的斜率无关,且
与直线l的斜率无关,且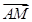 ·
· =-5.
=-5.另解:连结CA并延长交m于点B,连结CM,CN,由题意知AC⊥m,又CM⊥l,∴四点M、C、N、B都在以CN为直径的圆上,由相交弦定理,得
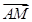 ·
· =-|AM|·|AN|=-|AC|·|AB|=-5.
=-|AM|·|AN|=-|AC|·|AB|=-5.
练习册系列答案
相关题目
 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切. 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的直线
的直线 垂直平分弦
垂直平分弦 ?
? 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 为圆上一点,过点
为圆上一点,过点 的延长线于点
的延长线于点 ,
, ,
, ,
, ,则
,则 ;圆的直径为 .
;圆的直径为 .
 ,若
,若 ,且
,且 ,则
,则 的取值范围为 .
的取值范围为 . ,则k的取值范围是________.
,则k的取值范围是________. 与曲线
与曲线 有公共点,则b的取值范围是 ( )
有公共点,则b的取值范围是 ( )



 ,则圆的方程为( )
,则圆的方程为( ) 2=
2=
 2+
2+