题目内容
已知圆心(a,b)(a<0,b<0)在直线y=2x+1上的圆,其圆心到x轴的距离恰好等于圆的半径,在y轴上截得的弦长为2 ,则圆的方程为( )
,则圆的方程为( )
 ,则圆的方程为( )
,则圆的方程为( )| A.(x+2)2+(y+3)2=9 | B.(x+3)2+(y+5)2=25 |
C.(x+6)2+ 2= 2= | D. 2+ 2+ 2= 2= |
A
由圆心到x轴的距离恰好等于圆的半径知,所求圆与x轴相切,由题意得圆的半径为|b|,则圆的方程为(x-a)2+(y-b)2=b2.由于圆心在直线y=2x+1上,得b=2a+1 ①,令x=0,得(y-b)2=b2-a2,此时在y轴上截得的弦长为|y1-y2|=2  ,由已知得,2
,由已知得,2  =2
=2 ,即b2-a2=5 ②,由①②得
,即b2-a2=5 ②,由①②得 或
或 (舍去).所以,所求圆的方程为(x+2)2+(y+3)2=9.故选A.
(舍去).所以,所求圆的方程为(x+2)2+(y+3)2=9.故选A.
 ,由已知得,2
,由已知得,2  =2
=2 ,即b2-a2=5 ②,由①②得
,即b2-a2=5 ②,由①②得 或
或 (舍去).所以,所求圆的方程为(x+2)2+(y+3)2=9.故选A.
(舍去).所以,所求圆的方程为(x+2)2+(y+3)2=9.故选A.
练习册系列答案
相关题目
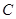 的方程为:
的方程为: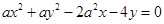 (
(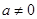 ,
,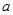 为常数).
为常数).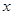 轴、
轴、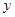 轴交于点
轴交于点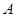 、
、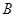 (
(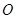 ),试判断
),试判断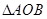 的面积
的面积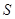 是否为定值?并证明你的判断;
是否为定值?并证明你的判断;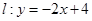 与曲线
与曲线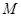 、
、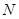 ,且
,且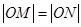 ,求曲线
,求曲线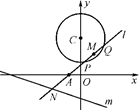
 时,求直线l的方程;
时,求直线l的方程;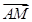 ·
· 是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.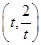 为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点. 与圆
与圆 相交于
相交于 、
、 两点且
两点且 ,则
,则 __________________;
__________________;  始终平分圆
始终平分圆 的周长,则
的周长,则 的取值范围是( )
的取值范围是( ) ·
· =( )
=( )