题目内容
10.函数f(x)=$\sqrt{3}$cos2$\frac{x}{2}$-$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$(x∈[0,π])的单调递增区间为( )| A. | [0,$\frac{5π}{6}$] | B. | [0,$\frac{2π}{3}$] | C. | [$\frac{5π}{6}$,π] | D. | [$\frac{2π}{3}$,π] |
分析 利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;可得x∈[0,π]的单调递增区间.
解答 解:函数f(x)=$\sqrt{3}$cos2$\frac{x}{2}$-$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$(x∈[0,π])
化简可得:f(x)=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$=cos(x+$\frac{π}{6}$)
由-π+2kπ≤x+$\frac{π}{6}$≤2kπ.
可得:$-\frac{7π}{6}+2kπ≤$x≤$2kπ-\frac{π}{6}$,k∈Z.
∵x∈[0,π],
当k=1时,可得增区间为[$\frac{5π}{6}$,π].
故选C.
点评 本题主要考查三角函数的图象和性质,属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
20.已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2,则a的值为( )
| A. | 1 | B. | 3 | C. | $\frac{1}{2}$ | D. | 5 |
18.在2,0,1,7这组数据中,随机取出三个不同的数,则数字2是取出的三个不同数的中位数的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
5.如图是求12+22+32+…+1002的程序框图,则图中的①②分别是( )
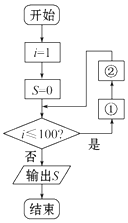

| A. | ①S=S+i ②i=i+1 | B. | ①S=S+i2 ②i=i+1 | C. | ①i=i+1 ②S=S+i | D. | ①i=i+1 ②S=S+i2 |

 如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中DD1=1,AB=BC=AA1=2,若此几何体的俯视图如图2所示,则可以作为其正视图的是( )
如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中DD1=1,AB=BC=AA1=2,若此几何体的俯视图如图2所示,则可以作为其正视图的是( )


