题目内容
利用判别式求函数y=
的值域.
| x |
| x2-3x+1 |
考点:函数的值域
专题:函数的性质及应用
分析:把函数化为yx2-(3y+1)x+y=0,利用判别式△≥0,求出y的取值范围即可.
解答:
解:∵函数y=
,
∴当x=0时,y=0;
当y≠0时,原函数化为yx2-(3y+1)x+y=0,
∴判别式△=(3y+1)2-4y2≥0,
即5y2+6y+1≥0;
解得y≤-1,或y≥-
,
综上,函数y的值域是{y|y≤-1,或y≥-
}.
| x |
| x2-3x+1 |
∴当x=0时,y=0;
当y≠0时,原函数化为yx2-(3y+1)x+y=0,
∴判别式△=(3y+1)2-4y2≥0,
即5y2+6y+1≥0;
解得y≤-1,或y≥-
| 1 |
| 5 |
综上,函数y的值域是{y|y≤-1,或y≥-
| 1 |
| 5 |
点评:本题考查了求函数值域的问题,利用判别式△≥0,可以求出函数y的值域,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
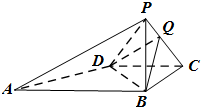 已知四面体P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD=
已知四面体P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD=
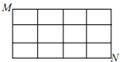 如图,在某个城市中,M,N两地之间有南北街道5条、东西街道4条,现要求沿图中的街道,以最短的路程从M走到N,则不同的走法共有
如图,在某个城市中,M,N两地之间有南北街道5条、东西街道4条,现要求沿图中的街道,以最短的路程从M走到N,则不同的走法共有