题目内容
 如图所示,正方形ABCD所在的平面与等腰△ABE所在的平面互相垂直,其中顶∠BAE=120°,AE=AB=4,F为线段AE的中点.
如图所示,正方形ABCD所在的平面与等腰△ABE所在的平面互相垂直,其中顶∠BAE=120°,AE=AB=4,F为线段AE的中点.(Ⅰ)若H是线段BD上的中点,求证:FH∥平面CDE;
(Ⅱ)若H是线段BD上的一个动点,设直线FH与平面ABCD所成角的大小为θ,求tanθ的最大值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)连接AC,证明FH∥CE,即可证明:FH∥平面CDE;
(Ⅱ)作FI⊥AB,垂足为I,则FI⊥AD,FI⊥平面ABCD,可得∠FHI是直线FH与平面ABCD所成角,tan∠FHI=
=
,当IH⊥BD时,IH取得最小值
,即可求tanθ的最大值.
(Ⅱ)作FI⊥AB,垂足为I,则FI⊥AD,FI⊥平面ABCD,可得∠FHI是直线FH与平面ABCD所成角,tan∠FHI=
| FI |
| IH |
| ||
| IH |
| 5 |
| 2 |
| 2 |
解答:
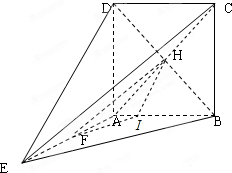 (Ⅰ)证明:连接AC,
(Ⅰ)证明:连接AC,
∵ABCD是正方形,
∴H是AC的中点,
∵F是AE的中点,
∴FH∥CE,
∵FH?平面CDE,CE?平面CDE,
∴FH∥平面CDE;
(Ⅱ)解:∵正方形ABCD所在的平面与等腰△ABE所在的平面互相垂直,DA⊥AB,
∴DA⊥平面ABE,
作FI⊥AB,垂足为I,则FI⊥AD,∴FI⊥平面ABCD,
∴∠FHI是直线FH与平面ABCD所成角.
∵FI=AFsin60°=
,
∴tan∠FHI=
=
,
当IH⊥BD时,IH取得最小值
,
∴(tan∠FHI)max=
.
 (Ⅰ)证明:连接AC,
(Ⅰ)证明:连接AC,∵ABCD是正方形,
∴H是AC的中点,
∵F是AE的中点,
∴FH∥CE,
∵FH?平面CDE,CE?平面CDE,
∴FH∥平面CDE;
(Ⅱ)解:∵正方形ABCD所在的平面与等腰△ABE所在的平面互相垂直,DA⊥AB,
∴DA⊥平面ABE,
作FI⊥AB,垂足为I,则FI⊥AD,∴FI⊥平面ABCD,
∴∠FHI是直线FH与平面ABCD所成角.
∵FI=AFsin60°=
| 3 |
∴tan∠FHI=
| FI |
| IH |
| ||
| IH |
当IH⊥BD时,IH取得最小值
| 5 |
| 2 |
| 2 |
∴(tan∠FHI)max=
| ||
| 5 |
点评:本题考查线面平行,考查直线FH与平面ABCD所成角,正确运用线面平行的判定定理,作出线面角是关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
已知方程kx+3-2k=
有两个不同的解,则实数k的取值范围是( )
| 4-x2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
数列{
}的前n项和为Sn,且满足a1=1,an=an-1+n,(n≥2),则Sn等于( )
| an |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
用a,b表示两条不同的直线,γ表示平面,给出下列命题:
(1)若a∥γ,b∥γ,则a∥b
(2)若a∥b,b∥γ,则a∥γ
(3)若a⊥γ,b∥γ,则a⊥b
(4)若a⊥γ,b⊥γ,则a∥b
其中真命题的序号是( )
(1)若a∥γ,b∥γ,则a∥b
(2)若a∥b,b∥γ,则a∥γ
(3)若a⊥γ,b∥γ,则a⊥b
(4)若a⊥γ,b⊥γ,则a∥b
其中真命题的序号是( )
| A、(1)(4) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(2) |