题目内容
8.设函数f(x)=(2-t)•2x+(t-3),其中t为常数,且t∈R.(1)求f(0)的值;
(2)求函数g(x)=$\frac{f(x)}{{4}^{x}}$在区间[0,1]上的最小值;
(3)若对任意实数t∈[-1,1],不等式f(x)>0恒成立.求实数x的取值范围.
分析 (1)代入可得
(2)求出g(x)=(2-t)($\frac{1}{2}$)x+(t-3)($\frac{1}{2}$)2xd配方得:=(t-3)[($\frac{1}{2}$)x+$\frac{2-t}{2(t-3)}$]2-$\frac{(2-t)^{2}}{4(t-3)}$,分别对t进行分类讨论可得函数的最小值;
(3)式子整理为t(2x-1)<2x+1-3,由t∈[-1,1],要使恒成立,则2x+1-3>2x-1且2x+1-3>-2x+1,分别求解求出x的范围.
解答 解:(1)f(0)=(2-t)+t-3
=-1;
(2)g(x)=(2-t)($\frac{1}{2}$)x+(t-3)($\frac{1}{2}$)2x
=(t-3)[($\frac{1}{2}$)2x+$\frac{2-t}{t-3}$]
=(t-3)[($\frac{1}{2}$)x+$\frac{2-t}{2(t-3)}$]2-$\frac{(2-t)^{2}}{4(t-3)}$
对称轴为x=-$\frac{2-t}{2(t-3)}$,($\frac{1}{2}$)x∈[$\frac{1}{2}$,1]
当3≤t≤4时,g(x)min=-$\frac{(2-t)^{2}}{4(t-3)}$
当t≥4时,g(x)min=g(1)=-1
当t<3时,g(x)min=g($\frac{1}{2}$)=2t-8;
(3)2x+1-t2x+t-3>0
∴t(2x-1)<2x+1-3
∵t∈[-1,1]
∴2x+1-3>2x-1且2x+1-3>-2x+1
解得x>$lo{g}_{2}\frac{4}{3}$且x>1
故x的范围为x>1.
点评 考察了二次函数的配方,参数的讨论以及对恒成立问题的理解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
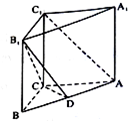 在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.