题目内容
3.已知函数f(x)=cosxsin2x,下列结论中正确的是①④(填入正确结论的序号)①y=f(x)的图象关于(2π,0)中心对称 ②y=f(x)的图象关于直线x=π对称 ③f(x)的最大值为$\frac{\sqrt{3}}{2}$
④f(x)既是奇函数,又是周期函数.
分析 ①用中心对称的充要条件,直接验证f(4π-x)+f(x)=0是否成立即可判断其正误;
②用轴对称的条件直接验证f(2π-x)=f(x)成立与否即可判断其正误;
③可将函数解析式换为f(x)=2sinx-2sin3x,再换元为y=2t-2t3,t∈[-1,1],利用导数求出函数在区间上的最值即可判断正误;
④可利用奇函数的定义与周期函数的定义直接证明.
解答 解:①∵f(4π-x)+f(x)=cos(4π-x)sin2(4π-x)+cosxsin2x=-cosxsin2x+cosxsin2x=0,
故y=f(x)的图象关于(2π,0)中心对称,故①正确,
②∵f(2π-x)=cos(2π-x)sin2(2π-x)=-cosxsin2x=-f(x),故y=f(x)的图象关于x=π不对称,故②错误,
③f(x)=cosxsin2x=2sinxcos2x=2sinx(1-sin2x)=2sinx-2sin3x,令t=sinx∈[-1,1],
则y=2t-2t3,t∈[-1,1],则y′=2-6t2,令y′>0解得$-\frac{\sqrt{3}}{3}<t<\frac{\sqrt{3}}{3}$,
故y=2t-2t3,在[$-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}$]上增,在[$-1,-\frac{\sqrt{3}}{3}$]与[$\frac{\sqrt{3}}{3},1$]上减,
又y(-1)=0,y($\frac{\sqrt{3}}{3}$)=$\frac{4\sqrt{3}}{9}$,故函数的最大值为$\frac{4\sqrt{3}}{9}$,故③错误;
④∵f(-x)+f(x)=-cosxsin2x+cosxsin2x=0,故是奇函数,
又f(x+2π)=cos(2π+x)sin2(2π+x)=cosxsin2x,故2π是函数的周期,
∴函数即是奇函数,又是周期函数,故④正确.
故正确的是①④,
故答案为:①④.
点评 本题考查函数的中心对称性,轴对称性的条件,利用导数求函数在闭区间上的最值,函数奇偶性与周期性的判定,涉及到的知识较多,综合性强.

 阅读快车系列答案
阅读快车系列答案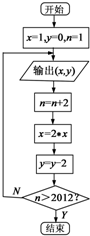 某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )| A. | 32 | B. | 24 | C. | 18 | D. | 16 |
| A. | Cn4 | B. | n!-3! | C. | Ann-3 | D. | Cnn-3 |