题目内容
19.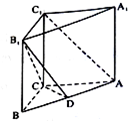 在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.(1)求证:AC⊥B1C;
(2)若D是AB中点,求证:AC1∥平面B1CD.
分析 (1)由题目给出的三棱柱的底面边长可证得AC⊥BC,再根据给出的三棱柱为直三棱柱,有AC⊥CC1,利用线面垂直的判定可以证明AC⊥面BB1C1C,从而得到要证的结论.(2)连结BC1,交B1C于E,连接DE.证明DE∥AC1,利用直线与平面平行的判定定理证明AC1∥平面B1CD.
解答 证明:(1)在△ABC中,∵AB=5,AC=4,BC=3,
∴AC2+BC2=AB2.
∴AC⊥BC.
∵直三棱柱ABC-A1B1C1,
∴CC1⊥AC.
∵BC∩C1C=C,
∴AC⊥平面BB1C1C.
∴AC⊥B1C.
(2)如图连接BC1,交B1C与E,连接DE,
∵直三棱柱ABC-A1B1C1,∴侧面BB1C1C为矩形,D是AB中点,DE为△ABC1的中位线,
∴DE∥AC1.
∵DE?平面B1CD,AC1?平面B1CD,∴AC1∥平面B1CD.
点评 本题主要考查了直线与平面垂直的性质,考查了直线与平面平行的判定定理的应用,考查空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
9.已知f(sinx)=3-cos2x,则f(cosx)=( )
| A. | 3-cos2x | B. | 3-sin2x | C. | 3+cos2x | D. | 3+sin2x |
14.4×5×6×…×(n-1)×n=( )
| A. | Cn4 | B. | n!-3! | C. | Ann-3 | D. | Cnn-3 |
4.设m>1,x,y满足约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$,且目标函数z=x+my的最大值为2,则m的取值为( )
| A. | 2 | B. | 1+$\sqrt{2}$ | C. | 3 | D. | 2+$\sqrt{2}$ |