题目内容
15.已知函数f(x)=2sin(ωx-$\frac{π}{3}$)(ω>0)与g(x)=cos(2x+φ)(0<φ<π)的图象对称轴完全相同,则g($\frac{π}{3}$)的值为$-\frac{{\sqrt{3}}}{2}$.分析 分别求得2个函数的图象的对称轴,根据题意可得ω=2,$\frac{5π}{12}$=$\frac{π}{2}$-$\frac{φ}{2}$,由此求得 φ 的值,可得g(x)的解析式,从而求得g($\frac{π}{3}$)的值.
解答 解:∵函数f(x)=2sin(ωx-$\frac{π}{3}$)(ω>0)的对称轴方程为ωx-$\frac{π}{3}$=kπ+$\frac{π}{2}$,即 x=$\frac{kπ}{ω}$+$\frac{5π}{6ω}$,k∈z.
g(x)=cos(2x+φ)(0<φ<π)的图象的对称轴为 2x+φ=kπ,即 x=$\frac{kπ}{2}$-$\frac{φ}{2}$,k∈z.
∵函数f(x)=2sin(ωx-$\frac{π}{3}$)(ω>0)和g(x)=cos(2x+φ)(0<φ<π)的图象的对称轴完全相同,
∴ω=2,再由0<φ<π,可得 $\frac{5π}{12}$=$\frac{π}{2}$-$\frac{φ}{2}$,
∴φ=$\frac{π}{6}$,
∴g(x)=cos(2x+φ)=cos(2x+$\frac{π}{6}$),g($\frac{π}{3}$)=cos$\frac{5π}{6}$=$-\frac{{\sqrt{3}}}{2}$.
故答案为:$-\frac{{\sqrt{3}}}{2}$.
点评 本题主要考查了三角函数的对称轴方程的求法,注意两个函数的对称轴方程相同的应用,找出一个对称轴方程就满足题意,考查计算能力,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
3.已知集合M={1,4},N={a,a+1},则满足条件M∩N≠∅的实数a组成的集合是( )
| A. | {1,4} | B. | {1,3} | C. | {1,3,4} | D. | {0,1,3,4} |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.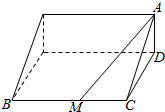 如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.
如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.