题目内容
10.若函数f(x)=x3+$\frac{3}{2}$x2+m在[-2,1]上的最大值为$\frac{9}{2}$,则实数m的值为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 由已知得y′=3x2+3x,由y′=0,得x=0或x=-1,由此利用导数性质求出函数f(x)=x3+$\frac{3}{2}$x2+m在[-2,1]上的最大值为f(1),由此能求出m的值.
解答 解:∵f(x)=x3+$\frac{3}{2}$x2+m,
∴f′(x)=3x2+3x,
由f′(x)=0,得x=0或x=-1,
∵f(-2)=m-2,f(-1)=$\frac{1}{2}$+m,f(0)=m,f(1)=$\frac{5}{2}$+m,
∴函数f(x)[-2,1]上的最大值为f(1)=$\frac{9}{2}$,
解得m=2,
故选:C.
点评 本题考查函数的最值的求法,是中档题,解题时要注意导数性质的合理运用.

练习册系列答案
相关题目
15.在平行四边形ABCD中,E、F分别是边CD和BC的中点,若$\overrightarrow{AC}=λ\overrightarrow{AE}+μ\overrightarrow{AF,}$其中λ,μ∈R,则λ+μ=( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | 1 |

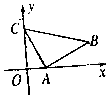
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,DD1⊥底面ABCD,E是DD1的中点
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,DD1⊥底面ABCD,E是DD1的中点