题目内容
15.在平行四边形ABCD中,E、F分别是边CD和BC的中点,若$\overrightarrow{AC}=λ\overrightarrow{AE}+μ\overrightarrow{AF,}$其中λ,μ∈R,则λ+μ=( )| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | 1 |
分析 推导出$\overrightarrow{AC}$=$\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AD}+\overrightarrow{AB}$,$\overrightarrow{AE}$=$\overrightarrow{AD}+\overrightarrow{DE}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$,从而$\overrightarrow{AC}$=$\overrightarrow{AD}+\overrightarrow{AB}$=($λ+\frac{1}{2}μ$)$\overrightarrow{AD}$+($\frac{1}{2}λ+μ$)$\overrightarrow{AB}$,由此能求出λ+μ.
解答 解: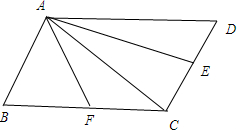 ∵在平行四边形ABCD中,E、F分别是边CD和BC的中点,
∵在平行四边形ABCD中,E、F分别是边CD和BC的中点,
∴$\overrightarrow{AC}$=$\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AD}+\overrightarrow{AB}$,
$\overrightarrow{AE}$=$\overrightarrow{AD}+\overrightarrow{DE}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,
$\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$,
∵$\overrightarrow{AC}=λ\overrightarrow{AE}+μ\overrightarrow{AF,}$其中λ,μ∈R,
∴$\overrightarrow{AC}$=$\overrightarrow{AD}+\overrightarrow{AB}$=λ($\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$)+μ($\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$)
=($λ+\frac{1}{2}μ$)$\overrightarrow{AD}$+($\frac{1}{2}λ+μ$)$\overrightarrow{AB}$,
∴$\left\{\begin{array}{l}{λ+\frac{1}{2}μ=1}\\{\frac{1}{2}λ+μ=1}\end{array}\right.$,∴$\frac{3}{2}$(λ+μ)=2,
解得λ+μ=$\frac{4}{3}$.
故选:C.
点评 本题考查代数式求和,考查平面向量等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则${∫}_{-1}^{1}$f(x)dx=( )
如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则${∫}_{-1}^{1}$f(x)dx=( )| A. | $\frac{π}{2}$+1 | B. | $\frac{π}{2}$+2 | C. | π+1 | D. | π+2 |
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-2,0)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
| A. | -$\frac{16}{25}$ | B. | -$\frac{7}{25}$ | C. | $\frac{7}{25}$ | D. | $\frac{16}{25}$ |