题目内容
18．过圆x2+y2-8x-2y+8=0内一点P（3，-1）的最长弦，最短弦所在的直线方程式分别是（ ）| A． | x-y-4=0，2x-y-7=0 | B． | 2x+y-5=0，x-2y-5=0 | ||
| C． | x-2y-1=0，2x-y-7=0 | D． | 2x-y-7=0，x+2y-1=0 |
分析 求出圆的圆心坐标，过圆内点P最长弦是直径，
最短弦所在的直线与最长弦所在的直线垂直，求出直线方程即可．
解答 解：圆x2+y2-8x-2y+8=0化为标准方程是
（x-4）2+（y-1）2=9，
∴该圆的圆心为I（4，1）；
则过圆内点P（3，-1）最长弦是直径，
其所在的直线方程是$\frac{x-3}{4-3}$=$\frac{y+1}{1+1}$，
化为一般式为2x-y-7=0；
最短弦所在的直线与最长弦所在的直线垂直，
直线方程的斜率为k=-$\frac{1}{2}$，
直线方程为y+1=-$\frac{1}{2}$（x-3），
化为一般式为x+2y-1=0．
故选：D．
点评 本题考查了直线与圆的方程应用问题，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
8．
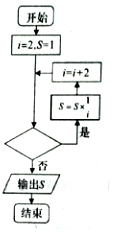如图，给出的是计算连乘数值的程序框图，其中判断框内不能填入（ ）
如图，给出的是计算连乘数值的程序框图，其中判断框内不能填入（ ）| A． | i≤2019？ | B． | i＜2019？ | C． | i≤2017？ | D． | i≤2018？ |
9．定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2）时，f（x）=$\left\{\begin{array}{l}{{x}^{2}-x，x∈[0，1）}\\{-（\frac{1}{2}）^{|x-\frac{3}{2}|}x∈[1，2）}\end{array}\right.$，若当x∈[-4，-2）时，不等式f（x）≥$\frac{{t}^{2}}{4}$-t+$\frac{1}{2}$恒成立，则实数t的取值范围是（ ）
| A． | [2，3] | B． | [1，3] | C． | [1，4] | D． | [2，4] |
3．已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，取DE的中点F，则$\overrightarrow{AF}•\overrightarrow{BC}$的值为（ ）
| A． | $-\frac{5}{8}$ | B． | $-\frac{1}{8}$ | C． | $\frac{1}{8}$ | D． | $\frac{11}{8}$ |
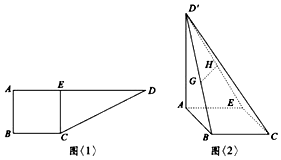如图＜1＞：在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2，AD=6，CE⊥AD于E点，把△DEC沿CE折到D'EC的位置，使$D'A=2\sqrt{3}$，如图＜2＞：若G，H分别为D'B，D'E的中点．