题目内容
4.函数y=g(x)的图象是由函数f(x)=sin2x-$\sqrt{3}$cos2x的图象向左平移$\frac{1}{6}$个周期而得到的,则函数y=g(x)的图象与直线x=0,x=$\frac{π}{3}$,x轴围成的封闭图形的面积为( )| A. | π | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
分析 利用两角和差的正弦公式化简f(x)的解析式,利用正弦函数的周期性,y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用定积分的几何意义,求得g(x)的图象与直线x=0,x=$\frac{π}{3}$,x轴围成的封闭图形的面积.
解答 解:函数f(x)=sin2x-$\sqrt{3}$cos2x=2sin(2x-$\frac{π}{3}$)的周期为$\frac{2π}{2}$=π,
∵函数y=g(x)的图象是由函数f(x)=sin2x-$\sqrt{3}$cos2x=2sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{1}{6}$个周期,
即向左平移$\frac{π}{6}$个单位而得到的,
∴g(x)=2sin(2x+$\frac{π}{3}$-$\frac{π}{3}$)=2sin2x,
故函数y=g(x)的图象与直线x=0,x=$\frac{π}{3}$,x轴围成的封闭图形的面积
S=${∫}_{0}^{\frac{π}{3}}$2sin2xdx=-cos2x${|}_{0}^{\frac{π}{3}}$=-cos$\frac{2π}{3}$-(-cos0)=$\frac{1}{2}$+1=$\frac{3}{2}$,
故选:C.
点评 本题主要考查两角和差的正弦公式,正弦函数的周期性,y=Asin(ωx+φ)的图象变换规律,定积分的几何意义,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
14.下列函数中,既是奇函数,又在定义域上是增函数的是( )
| A. | y=x2 | B. | y=x|x| | C. | y=x+$\frac{2}{x}$ | D. | y=x-$\frac{4}{x}$ |
15.已知双曲线的中心在原点,两个焦点F1,F2分别为$(-\sqrt{5},0)和(\sqrt{5},0)$,点P在双曲线上,PF1⊥PF2,且△PF1F2的面积为1,则双曲线的方程为( )
| A. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
12.已知正实数a,b满足a+b=3,则$\frac{1}{a}+\frac{4}{5+b}$的最小值为( )
| A. | 1 | B. | $\frac{7}{8}$ | C. | $\frac{9}{8}$ | D. | 2 |
16.已知Sn是公比为q的等比数列{an}的前n项和.若3S1,2S2,S3成等差数列,则q=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
13.设x,y∈N*,x+y=10,xy>20的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{9}$ |
14.一个正三棱柱的三视图如图所示,则这个正三棱柱的侧面积为( )
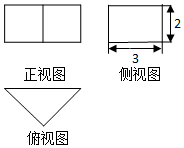

| A. | 18 | B. | $18\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $12\sqrt{3}$ |