题目内容
求
-
的值．
2
|
2+
|
考点：数列的求和,根式与分数指数幂的互化及其化简运算
专题：计算题,等差数列与等比数列
分析：令
=x，两边平方得x2=2x，或运用无穷递缩等比数列的求和公式Sn=
，再令
=y，两边平方得，y2=2+y，解出即可原式的值．
2
|
| a1 |
| 1-q |
2+
|
解答：
解：令
=x，两边平方得，x2=2x，x=2或x=0（舍去）．．
或x=2
•2
•2
•…=2
=2．
再令
=y，两边平方得，y2=2+y，y=2或y=-1（舍去）．
故原式=2-2=0．
2
|
或x=2
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| ||
1-
|
再令
2+
|
故原式=2-2=0．
点评：本题考查根式的运算与化简，考查两边平方求无穷式子的和，或者运用无穷递缩等比数列的求和公式，是一道中档题．
练习册系列答案
精英口算卡系列答案
相关题目
已知直线l1，l2和平面α，则l1∥l2的一个必要不充分的条件是（ ）
| A、l1∥α且l2∥α |
| B、l1⊥α且l2⊥α |
| C、l1∥α且l2?α |
| D、l1与l2成等角 |
设A表示一点，l，m表示两条不同的直线，α，β，γ表示三个不同的平面，给出下列四个命题：
①若l⊥α，m⊥l，m⊥β，则α⊥β；
②若m⊥α，m⊥β，则α∥β；
③若m是平面α的一条斜线，l为过A的一条动直线，则可能有l⊥m，l⊥α；
④若α⊥γ，β⊥γ，则α∥β；
其中真命题的序号是（ ）
①若l⊥α，m⊥l，m⊥β，则α⊥β；
②若m⊥α，m⊥β，则α∥β；
③若m是平面α的一条斜线，l为过A的一条动直线，则可能有l⊥m，l⊥α；
④若α⊥γ，β⊥γ，则α∥β；
其中真命题的序号是（ ）
| A、①② | B、①③ | C、②④ | D、③④ |
连续自然数按规律排成如图：根据规律，从2010到2012，箭头的方向依次为（ ）
| A、↓→ | B、→↑ | C、↑→ | D、→↓ |
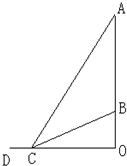如图，AB表示一座塑像，OB是塑像底座，塑像及其底座所在直线与地面垂直，已知AB=9m，OB=3m．