题目内容

函数y=2x2-4x+1的值域为
 
．
考点：函数的值域
专题：函数的性质及应用
分析：对式子x2-4x+1进行配方后求出范围，再由指数函数的单调性求出原函数的值域．
解答： 解：∵x2-4x+1=（x-2）2-3≥-3，且函数y=2x在R上是增函数，
∴y=2x2-4x+1≥2-3=
1
8
，
则函数y=2x2-4x+1的值域是[
1
8
，+∞），
故答案为：[
1
8
，+∞）．
点评：本题考查复合函数的值域的求法，指数函数的单调性，二次函数的性质，以及整体思想．
练习册系列答案
相关题目
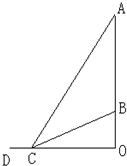判断方程2lnx+x-4=0在（1，e）内是否存在实数解，若存在，有几个实数解？
如图，AB表示一座塑像，OB是塑像底座，塑像及其底座所在直线与地面垂直，已知AB=9m，OB=3m．
（1）请用∠ACO与∠BCO的正切表示∠ACB的正切；
（2）在地面OD上求一点C，使C对塑像AB的视角∠ACB最大，这时OC长多少？
前不久，社科院发布了2013年度“全国城市居民幸福指数排行榜”，北京市称为本年度最“幸福城”．随后，某师大附中学生会组织部分同学，用“10份制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）．若幸福度不低于9.5分，则称该人的幸福度为“极幸福”．
（Ⅰ）求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
（Ⅱ）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记ξ表示抽到“极幸福”的人数，求ξ的分布列及数学期望．
设函数f（x）=ln（x+1）-
ax
x+1
，（a∈R）；g（x）=（1+k）x-kx-1，k∈（-1，+∞）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当x∈[0，1]时，求函数g（x）的最大值；
（Ⅲ）求证：
n
k=1
1
k+1
＜ln（n+1）＜
n
k=1
1
k
（n∈N*）
若函数f（x2）的定义域是[0，1]，则函数f（x）的定义域是
 
．
在△ABC中，角A，B，C所对应的边分别为a，b，c．已知bcosC+ccosB=2b，则
a
b
=
 
．
已知函数f（x）（x∈R）的图象如图所示，则函数g（x）=f（
x+1
x-1
）的单调递减区间是
 
．
若等差数列{an}的前n项和Sn满足：S4≤12，S9≥36，则a10的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网