题目内容
已知下面各数列{an}的前n项和Sn,求通项公式an
(1)Sn=2n2-3n
(2)Sn=3n-2.
(1)Sn=2n2-3n
(2)Sn=3n-2.
考点:等比数列的前n项和,数列的函数特性,等差数列的前n项和
专题:等差数列与等比数列
分析:利用an=
求解.
|
解答:
解:(1)∵Sn=2n2-3n,
∴a1=S1=2-3=-1,
当n≥2时,an=Sn-Sn-1=(2n2-3n)-[2(n-1)2-3(n-1)]
=4n-5.
n=1时,上式成立,
∴an=4n-5.
(2)∵Sn=3n-2,
∴a1=S1=3-2=1,
当n≥2时,
an=Sn-Sn-1=(3n-2)-(3n-1-2)=2•3n-1,
n=1时,上式不成立,
∴an=
.
∴a1=S1=2-3=-1,
当n≥2时,an=Sn-Sn-1=(2n2-3n)-[2(n-1)2-3(n-1)]
=4n-5.
n=1时,上式成立,
∴an=4n-5.
(2)∵Sn=3n-2,
∴a1=S1=3-2=1,
当n≥2时,
an=Sn-Sn-1=(3n-2)-(3n-1-2)=2•3n-1,
n=1时,上式不成立,
∴an=
|
点评:本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意公式an=
的合理运用.
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
连续自然数按规律排成如图:根据规律,从2010到2012,箭头的方向依次为( )


| A、↓→ | B、→↑ | C、↑→ | D、→↓ |
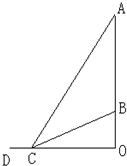 如图,AB表示一座塑像,OB是塑像底座,塑像及其底座所在直线与地面垂直,已知AB=9m,OB=3m.
如图,AB表示一座塑像,OB是塑像底座,塑像及其底座所在直线与地面垂直,已知AB=9m,OB=3m. 前不久,社科院发布了2013年度“全国城市居民幸福指数排行榜”,北京市称为本年度最“幸福城”.随后,某师大附中学生会组织部分同学,用“10份制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.
前不久,社科院发布了2013年度“全国城市居民幸福指数排行榜”,北京市称为本年度最“幸福城”.随后,某师大附中学生会组织部分同学,用“10份制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).若幸福度不低于9.5分,则称该人的幸福度为“极幸福”. 已知函数f(x)(x∈R)的图象如图所示,则函数g(x)=f(
已知函数f(x)(x∈R)的图象如图所示,则函数g(x)=f(