题目内容
15.函数f(x)=-$\frac{1}{x}$+cos(2x+$\frac{2π}{3}$)的一个零点所在的区间可以是( )| A. | (0,$\frac{π}{2}$) | B. | ($\frac{π}{2},\frac{2π}{3}$) | C. | ($π,\frac{7π}{6}$) | D. | ($\frac{4π}{3},\frac{7π}{6}$) |
分析 将各区间端点值代入f(x),若函数值异号,则在该区间内存在零点.
解答 解:当x→0+时,f(x)=-$\frac{1}{x}$+cos(2x+$\frac{2π}{3}$)→-∞<0,
f($\frac{π}{2}$)=-$\frac{2}{π}$+cos$\frac{5π}{3}$=$-\frac{2}{π}$+$\frac{1}{2}$<0,
f($\frac{2π}{3}$)=-$\frac{3}{2π}$+cos2π=-$\frac{3}{2π}$+1>0.
∴f($\frac{π}{2}$)•f($\frac{2π}{3}$)<0,即f(x)的一个零点所在区间为($\frac{π}{2}$,$\frac{2π}{3}$).
故选B.
点评 本题考查了零点的存在性定理,是基础题.

练习册系列答案
相关题目
7.从混有5张假钞的20张一百元纸币中任意抽取2张,将其中一张在验钞机上检验发现是假币,则这两张都是假币的概率为( )
| A. | $\frac{1}{19}$ | B. | $\frac{17}{18}$ | C. | $\frac{4}{19}$ | D. | $\frac{2}{17}$ |
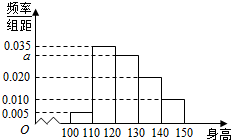 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取36人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为( )
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取36人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为( )