题目内容
13.2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的是( )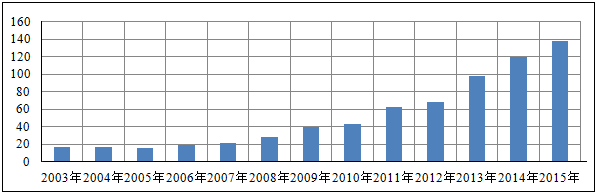
| A. | f(x)=ax2+bx+c | B. | f(x)=aex+b | C. | f(x)=eax+b | D. | f(x)=alnx+b |
分析 由图象可得:这13年间电影放映场次逐年变化规律的是随着x的增大,f(x)逐渐增大,图象逐渐上升.根据函数的单调性与图象的特征即可判断出结论.
解答 解:由图象可得:这13年间电影放映场次逐年变化规律的是随着x的增大,f(x)逐渐增大,图象逐渐上升.
对于A.f(x)=ax2+bx+c,取a>0,$-\frac{b}{2a}$<0,可得满足条件的函数;
对于B.取a>0,b>0,可得满足条件的函数;
对于C.取a>0,b>0,可得满足条件的函数;
对于D.a>0时,为“上凸函数”,不符合图象的特征;a<0时,为单调递减函数,不符合图象的特征.
故选:D.
点评 本题考查了函数的图象与性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.一个几何体的三视图如图所示,则此几何体的体积为( )
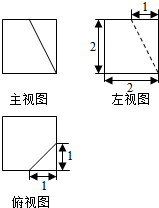

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{23}{3}$ | D. | $\frac{22}{3}$ |
5.设a=e0.3,b=0.92,c=ln0.9,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |