题目内容
1.已知tan2α+cot2α=m(cotα=$\frac{1}{tanα}$),则tanα+cotα的值为±$\sqrt{m+2}$.分析 设tanα+cotα=t,则平方可得 t2=tan2α+cot2α+2=m+2,由此求得t的值.
解答 解:设tanα+cotα=t,则平方可得 t2=tan2α+cot2α+2=m+2,
∴t=±$\sqrt{m+2}$,故答案为:±$\sqrt{m+2}$.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
13.在△ABC中,cosAcosB=0,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
13.2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的是( )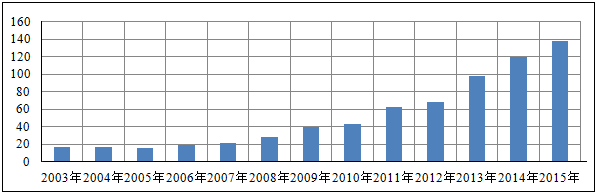

| A. | f(x)=ax2+bx+c | B. | f(x)=aex+b | C. | f(x)=eax+b | D. | f(x)=alnx+b |