题目内容
已知a=(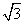 ,cosx),b=(cos2x,sinx),函数f(x)=a·b-
,cosx),b=(cos2x,sinx),函数f(x)=a·b-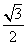 .
.
(1)求函数f(x)的单调递增区间;
(2)若x∈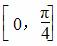 ,求函数f(x)的取值范围;
,求函数f(x)的取值范围;
(3)函数f(x)的图象经过怎样的平移可使其对应的函数成为奇函数.
(1)函数f(x)=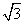 cos2x+sinxcosx-
cos2x+sinxcosx-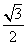
=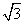
 +
+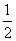 sin2x-
sin2x-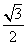
=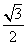 cos2x+
cos2x+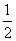 sin2x=sin
sin2x=sin ,
,
由- +2kπ≤2x+
+2kπ≤2x+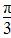 ≤
≤ +2kπ,k∈Z得,
+2kπ,k∈Z得,
- +kπ≤x≤
+kπ≤x≤ +kπ,k∈Z,
+kπ,k∈Z,
所以f(x)的单调递增区间为 ,(k∈Z).
,(k∈Z).
(2) 
∴当2x+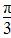 =
= 即x=
即x= 时,f(x)max=1,
时,f(x)max=1,
当2x+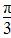 =
=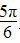 即x=
即x= 时,f(x)min=
时,f(x)min=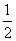 ,∴
,∴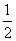 ≤f(x)≤1.
≤f(x)≤1.
(3)将f(x)的图象上所有的点向右平移 个单位长度得到y=sin2x的图象,则其对应的函数即为奇函数.(答案不唯一)
个单位长度得到y=sin2x的图象,则其对应的函数即为奇函数.(答案不唯一)

练习册系列答案
相关题目

 -θ)+cos(π+θ)=0,则cos2θ+
-θ)+cos(π+θ)=0,则cos2θ+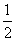 sin2θ的值是________.
sin2θ的值是________.
 D.
D.
 个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )
个单位后,得到一个偶函数的图象,则φ的一个可能取值为( ) B.
B. 
 sinC,B=30°,那么角A等于( )
sinC,B=30°,那么角A等于( ) )-cos2x+m.
)-cos2x+m. 时,函数f(x)的最小值为-3,求实数m的值.
时,函数f(x)的最小值为-3,求实数m的值.