题目内容
16.已知x=log23-log2$\sqrt{3}$,y=log0.53,z=0.9-1.1,则( )| A. | x<y<z | B. | z<y<x | C. | y<z<x | D. | y<x<z |
分析 利用对数函数和指数函数的单调性即可得出.
解答 解:∵y=log0.53<log0.51=0,
0<xlog23-log2$\sqrt{3}$=log2$\sqrt{3}$<1,
z=0.9-1.1>0.90=1.
∴y<x<z.
故选:D.
点评 本题考查了对数函数和指数函数的单调性,属于基础题.

练习册系列答案
相关题目
6.已知m,n是两条不同直线,α,β是两个不同平面,则下列命题错误的是( )
| A. | 若α,β垂直于同一平面,则α与β可能相交 | |
| B. | 若m,n平行于同一平面,则m与n可能异面 | |
| C. | 若m,n不平行,则m与n不可能垂直于同一平面 | |
| D. | 若α,β不平行,则在α内不存在与β平行的直线 |
7.已知扇形OAB的圆心角为4,其面积是2cm2则该扇形的周长是( )
| A. | 8cm | B. | 6cm | C. | 4cm | D. | 2cm |
4.若点P是曲线y=2x-ex上任意一点,则点P到直线y=x的最小距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
11.函数f(x)=ln(1+2x),g(x)=ln(1-2x),则f(x)+g(x)为( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既不是奇函数又不是偶函数 | D. | 既是奇函数又是偶函数 |
1.已知随机变量X满足D(X)=3,则D(3X+2)=( )
| A. | 2 | B. | 27 | C. | 18 | D. | 20 |
5.给出一个程序框如图,则输出x的值是( )


| A. | 45 | B. | 43 | C. | 41 | D. | 39 |
6.某几何体的三视图如图所示,则该三视图的体积为( )
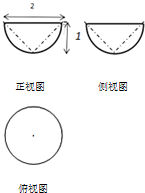

| A. | $\frac{π}{3}$ | B. | $\frac{4}{3}$π | C. | 2π | D. | $\frac{8}{3}$π |