题目内容

16．设复数z=-2+i（i是虚数单位），z的共轭复数为$\overline{z}$，则|（1+z）•$\overline{z}$|等于（　　）
A．$\sqrt{5}$B．2$\sqrt{5}$C．5$\sqrt{2}$D．$\sqrt{10}$

分析 求出z的共轭复数，代入|（1+z）•$\overline{z}$，求出其模即可．

解答 解：∵z=-2+i，∴$\overline{z}$=-2-i，
∴|（1+z）•$\overline{z}$|=|（1-2+i）•（2-i）|=|-1+3i|=$\sqrt{1+9}$=$\sqrt{10}$，
故选：D．

点评 本题考查了复数求模问题，考查共轭复数问题，是一道基础题．

练习册系列答案
相关题目
6．已知△ABC是边长为$2\sqrt{3}$的正三角形，EF为△ABC的外接圆O的一条直径，M为△ABC的边上的动点，则$\overrightarrow{ME}•\overrightarrow{FM}$的最大值为（　　）
A．3B．4C．5D．6
7．已知集合A={x|（x-3）（x+1）＜0}，B={x|x＞1}，则A∩B=（　　）
A．{x|x＞3}B．{x|x＞1}C．{x|-1＜x＜3}D．{x|1＜x＜3}
4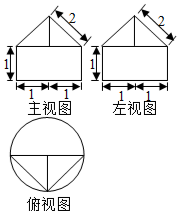．一个几何体的三视图如图所示，则该几何体的体积为（　　）
A．2π+$\frac{\sqrt{3}}{3}$B．π+$\frac{\sqrt{3}}{3}$C．2π+$\frac{\sqrt{3}}{3}$D．π+$\sqrt{3}$
11．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为4π，且其图象向右平移$\frac{π}{7}$个单位后得到函数g（x）=sinωx的图象，则φ等于（　　）
A．-$\frac{π}{14}$B．-$\frac{π}{7}$C．$\frac{π}{14}$D．$\frac{π}{7}$
1．设集合M={x|x=2n，n∈Z}，N={x|x=2n+1，n∈Z}，P={x|x=4n，n∈Z}，则（　　）
A．M=PB．P≠MC．N∩P≠∅D．M∩N≠∅
8．设F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的右焦点，若点F关于双曲线的一条渐近线的对称点P恰好落在双曲线的左支上，则双曲线的离心率为$\sqrt{5}$．
5．已知点$P（\sqrt{3}，1）$，Q（cosx，sinx），O为坐标原点，函数$f（x）=\overrightarrow{OP}•\overrightarrow{QP}$．
（1）求函数f（x）的最小值及此时x的值；
（2）若A为△ABC的内角，f（A）=4，BC=3，求△ABC的周长的最大值．
6．已知${log_a}b=-1，\;{2^a}＞3，\;c＞1$，设$x=-{log_b}\sqrt{a}$，y=logbc，$z=\frac{1}{3}a$，则x，y，z的大小关系正确的是（　　）
A．z＞x＞yB．z＞y＞xC．x＞y＞zD．x＞z＞y

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网