题目内容
若m、n表示直线,α、β表示平面,则下列四个命题中:
(1)若m∥α,则对任意的n?α,都有m∥n
(2)若实数t1,t2满足t1•t2≠6,则t1≠2或t2≠3
(3)若k>3,则方程
-
=1表示双曲线
(4)若α⊥β,α∩β=l,m⊥l,则m⊥β
正确命题是 (请填正确的序号)
(1)若m∥α,则对任意的n?α,都有m∥n
(2)若实数t1,t2满足t1•t2≠6,则t1≠2或t2≠3
(3)若k>3,则方程
| x2 |
| k-3 |
| y2 |
| k+3 |
(4)若α⊥β,α∩β=l,m⊥l,则m⊥β
正确命题是
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:(1)由m∥α,对任意的n?α,利用线面平行的性质定理可得:m∥n或为异面直线;
(2)由实数t1,t2满足t1•t2≠6,可利用其逆否命题t1≠2或t2≠3;
(3)由k>3,可得k+3>0,k-3>0,利用双曲线的标准方程即可判断出;
(4)利用面面垂直的性质定理即可得出.
(2)由实数t1,t2满足t1•t2≠6,可利用其逆否命题t1≠2或t2≠3;
(3)由k>3,可得k+3>0,k-3>0,利用双曲线的标准方程即可判断出;
(4)利用面面垂直的性质定理即可得出.
解答:
解:(1)若m∥α,则对任意的n?α,则m∥n或为异面直线,因此不正确;
(2)若实数t1,t2满足t1•t2≠6,利用逆否命题可知t1≠2或t2≠3,正确;
(3)若k>3,则k+3>0,k-3>0,可得方程
-
=1表示双曲线,正确;
(4)若α⊥β,α∩β=l,m⊥l,若m?α或m∥α,才可能有m⊥β,因此不正确.
综上可知:只有(2)(3)正确.
故答案为:(2)(3).
(2)若实数t1,t2满足t1•t2≠6,利用逆否命题可知t1≠2或t2≠3,正确;
(3)若k>3,则k+3>0,k-3>0,可得方程
| x2 |
| k-3 |
| y2 |
| k+3 |
(4)若α⊥β,α∩β=l,m⊥l,若m?α或m∥α,才可能有m⊥β,因此不正确.
综上可知:只有(2)(3)正确.
故答案为:(2)(3).
点评:本题综合考查了线面、面面平行与垂直的性质定理、双曲线的标准方程等基础知识,属于基础题.

练习册系列答案
相关题目
将函数f(x)=
sin2x-cos2x的图象向左平移|m|个单位(m>-
),若所得的图象关于直线x=
对称,则m的最小值为( )
| 3 |
| π |
| 2 |
| π |
| 6 |
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
在复平面内,复数z满足(3-4i)z=|4+3i|(i为虚数单位),则z的虚部为( )
| A、-4 | ||
B、-
| ||
| C、4 | ||
D、
|
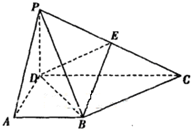 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2. 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: