题目内容
化简:
(1)
+
+
.
(2)
+
.
(3)0.064 -
-(-
)0+16
+0.25
.
(4)
.
(1)
3-2
|
| 3 | (1-
| ||
| 4 | (1-
| ||
(2)
| 3 | 2+
| ||
| 3 | 2-
| ||
(3)0.064 -
| 1 |
| 3 |
| 1 |
| 16 |
| 3 |
| 4 |
| 1 |
| 2 |
(4)
| a-1+b-1 |
| (ab)-1 |
考点:有理数指数幂的化简求值,根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:(1)利用根式的运算性质即可得出.
(2)令x=
+
,利用“立方和公式”即可得出;
(3)利用指数幂的运算公式即可得出.
(4)利用指数幂的运算性质即可得出.
(2)令x=
| 3 | 2+
| ||
| 3 | 2-
| ||
(3)利用指数幂的运算公式即可得出.
(4)利用指数幂的运算性质即可得出.
解答:
解:(1)原式=
-1+1-
+
-1=
-1.
(2)令x=
+
,则x3=2+
+2-
+3
•
x,化为x3+3x-4=0,因式分解为(x-1)(x2+x+4)=0,解得x=1.
(3)原式=0.43×(-
)-1+24×
+(
)2×
=
-1+8+
=10.
(4)原式=
=a+b.
| 2 |
| 2 |
| 2 |
| 2 |
(2)令x=
| 3 | 2+
| ||
| 3 | 2-
| ||
| 5 |
| 5 |
| 3 | 2+
| ||
| 3 | 2-
| ||
(3)原式=0.43×(-
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 5 |
| 2 |
| 1 |
| 2 |
=10.
(4)原式=
(
| ||||
|
点评:本题考查了指数幂的运算性质、乘法公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
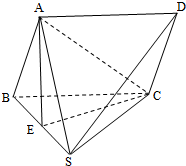 如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧SBC是正三角形,点E是SB的中点,且AE⊥平面ABC.
如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧SBC是正三角形,点E是SB的中点,且AE⊥平面ABC.(1)证明:SD∥平面ACE;
(2)若AB⊥AS,BC=2,求点S到平面ABC的距离.
空间直线a、b、c,平面α,则下列命题中真命题的是( ):
| A、若a⊥b,c⊥b,则a∥c |
| B、若a∥c,c⊥b,则b⊥a |
| C、若a与b是异面直线,a与c是异面直线,则b与c也是异面直线. |
| D、若a∥α,b∥α,则a∥b |
已知m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
| A、若α⊥β,m∥α,则m⊥β |
| B、若m∥α,n∥β,且m∥n,则α∥β |
| C、若m⊥β,α⊥β,则m∥α |
| D、若m⊥α,n⊥β,且m⊥n,则α⊥β |
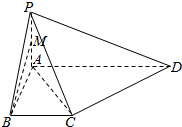 如图,已知PA⊥平面ABCD,AP=AB=BC=
如图,已知PA⊥平面ABCD,AP=AB=BC=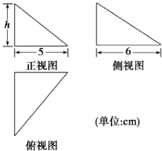 图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=
图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=