题目内容
6.某几何体的三视图如图所示,则该几何体的体积为( )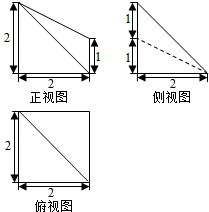
| A. | 8 | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{14}{3}$ |
分析 根据几何体的三视图,得出该几何体是四棱锥与三棱锥的组合体,画出图形结合图形求出它的体积.
解答 解:根据几何体的三视图,得;
该几何体是直四棱锥与三棱锥的组合体,画出图形如图所示;
则该几何体的体积为
V=V四棱锥P-ABCD+V三棱锥P-BCE
=$\frac{1}{3}$×2×2×2+$\frac{1}{3}$×$\frac{1}{2}$×2×1×2
=$\frac{10}{3}$.
故选:C.
点评 本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.若椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上有n个不同的点P1,P2,P3,…,Pn,F是右焦点,{|PnF|}组成等差数列,且公差d>$\frac{1}{100}$,则n的最大值是( )
| A. | 199 | B. | 200 | C. | 99 | D. | 100 |
17.已知某几何体的三视图如图,其中主视图中半圆的直径为2,则该几何体的表面积为( )

| A. | 46 | B. | 52-π | C. | 52+3π | D. | 46+2π |
14.某地区2007年至2013年居民人均纯收入y(单位:千元)的数据如表:
(1)设y关于t的线性回归方程为y=bt+a,求b,a的值;
(2)利用(1)中的回归方程,预测该地区2016年居民人均纯收入.
(参考公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,a=$\overline{y}$-b$\overline{t}$)
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(2)利用(1)中的回归方程,预测该地区2016年居民人均纯收入.
(参考公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,a=$\overline{y}$-b$\overline{t}$)
18.函数f(x)=lnx-x2+4x+5的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
15.若a,b是任意的实数,且a>b,则( )
| A. | |a|>|b| | B. | $\frac{b}{a}<1$ | C. | lga<lgb | D. | ${(\frac{1}{2})^a}<{(\frac{1}{2})^b}$ |