题目内容
16.已知函数f(x)=-x3+3x2+9x+a.(1)求f(x)的单调递减区间;
(2)若f(x)≥2015对于?x∈[-2,2]恒成立,求a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,从而求出函数的递减区间;
(2)问题转化为a≥x3-3x2-9x+2015对于?x∈[-2,2]恒成立,设g(x)=x3-3x2-9x+2015,x∈[-2,2],通过求导得到g(x)的最大值,从而求出a的范围即可.
解答 解:(1)f′(x)=-3x2+6x+9=-3(x2-2x-3)=-3(x-3)(x+1),
令f′(x)<0,解得:x>3或x<-1,
∴f(x)在(-∞,-1),(3,+∞)递减;
(2)f(x)≥2015对于?x∈[-2,2]恒成立
?a≥x3-3x2-9x+2015对于?x∈[-2,2]恒成立,
设g(x)=x3-3x2-9x+2015,x∈[-2,2],
则g′(x)=3(x-3)(x+1),
令g′(x)>0,解得:x<-1,
令g′(x)<0,解得:x>-1,
∴g(x)在[-2,-1)递增,在(-1,2]递减,
∴g(x)最大值=g(-1)=2020,
∴a≥2020.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,函数恒成立问题,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.某几何体的三视图如图所示,则该几何体的体积为( )
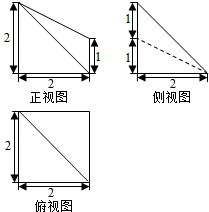

| A. | 8 | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{14}{3}$ |
1.设F是椭圆E:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$的左焦点,过点F且倾斜角为150°的直线l交椭圆E于M,N两点,连接MO(O为坐标原点)并延长交椭圆于P,则△MNP面积为( )
| A. | $\frac{5}{2}$ | B. | 5 | C. | $\frac{15}{2}$ | D. | 10 |
8.在等比数列{an}中,已知a2•a6=16,则a4=( )
| A. | 4 | B. | -4 | C. | 8 | D. | ±4 |
6.在△ABC中,角A,B满足sin$\frac{3A}{2}$=sin$\frac{3B}{2}$,则三边a,b,c必满足( )
| A. | a=b | B. | a=b=c | ||
| C. | a+b=2c | D. | (a-b)(a2+b2-ab-c2)=0 |
 如图1,已知ABCD是上、下底边长分别为2和6的等腰梯形.将它沿对称轴OO1折成直二面角,如图2,满足AC⊥BO1.
如图1,已知ABCD是上、下底边长分别为2和6的等腰梯形.将它沿对称轴OO1折成直二面角,如图2,满足AC⊥BO1.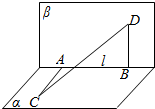 已知A,B是直二面角α-l-β的棱上两点,线段AC⊆α,线段BD⊆β,且AC⊥l,BD⊥l,AC=AB=6,BD=24,求线段CD的长.
已知A,B是直二面角α-l-β的棱上两点,线段AC⊆α,线段BD⊆β,且AC⊥l,BD⊥l,AC=AB=6,BD=24,求线段CD的长.