��Ŀ����
18��������Ѷ��˾�Ƴ���һ���ֻ�ͨѶ��������֧�ַ����������š���Ƶ��ͼƬ�����֣�һ���Ƴ������ȫ��������ӿ�ֳ�һ�����ŵ�����Ȧ��������Ʒ���ˣ�����Ϊ�̣���Ϊ�˵���ÿ�����û�ʹ���ŵ�ʱ�䣬ij������ױƷ������һ�㳡����ɷ����ԡ�Ů���û���50 ��������ÿ�����ų���6 Сʱ���û���Ϊ���ſء����������Ϊ�����ſء������������£�| �ſ� | ���ſ� | �ϼ� | |
| ���� | 26 | 24 | 50 |
| �� | 30 | 20 | 50 |
| �ϼ� | 56 | 44 | 100 |
��2���ִӵ����Ů���û��а��ֲ�����ķ���ѡ��5 �˲���ѡ����5 �����������ȡ3 ������200 Ԫ�Ļ���Ʒ��װ������3 ���С��ſء�������ΪX������X �ķֲ�������ѧ������
�ο���ʽ��${K^2}=\frac{{n{{��ad-bc��}^2}}}{��a+b����c+d����a+c����b+d��}$������n=a+b+c+d��
| P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
���� ��1��������������K2�������ٽ�ֵ�����ɵó����ۣ�
��2������������ȡ��5λŮ���С��ſء���3�ˣ���X�����п���ȡֵ��
�����Ӧ�ĸ��ʣ�д��X �ķֲ��У�������ѧ����ֵ��
��� �⣺��1������������֪��
${K^2}=\frac{{n{{��ad-bc��}^2}}}{��a+b����c+d����a+c����b+d��}$=$\frac{100{����26��20-30��24��}^{2}}{56��44��50��50}$=$\frac{50}{77}$��0.649��
��0.649��0.708��
��û��60%�İ�����Ϊ���ſء��롱�Ա��йأ�
��2��������֪������ȡ��5λŮ���С��ſء���3�ˣ�
�����ſء���2�ˣ�
��X�����п���ȡֵΪ1��2��3��
��P��X=1��=$\frac{{C}_{3}^{1}{•C}_{2}^{2}}{{C}_{5}^{3}}$=$\frac{3}{10}$��P��X=2��=$\frac{{C}_{3}^{2}{•C}_{2}^{1}}{{C}_{5}^{3}}$=$\frac{3}{5}$��P��X=3��=$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{1}{10}$��
��X �ķֲ���Ϊ��
| X | 1 | 2 | 3 |
| P��X�� | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
���� ���⿼���˶����Լ�������������ķֲ��к���ѧ�����ļ������⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
�����Ŀ
8����֪����f��x��=m��x+m+3����x+m+2����g��x��=2x-2����?x��R��f��x����0��g��x����0���������ʵ��m��ȡֵ��ΧΪ��������
| A�� | ��-3��0�� | B�� | ��-2��0�� | C�� | ��-3��-2�� | D�� | ��0��3�� |
9����֪��ABC�У�a=1��$b=\sqrt{3}$��A=30�㣬��B���ڣ�������
| A�� | 30�� | B�� | 30���150�� | C�� | 60�� | D�� | 60���120�� |
13��ij�����ͼ��ͼ��ʾ�����ó������к������ֵ��$\frac{25}{13}$��������
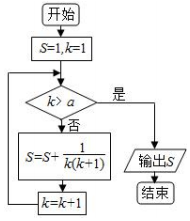

| A�� | a=11 | B�� | a=12 | C�� | a=13 | D�� | a=14 |
3��������R�ϵ���������f��x������f��1��=2����f��x����R�ϵĵ�����f�䣨x����1����ʽf��x����x+1�Ľ⼯Ϊ{x|x��1}��
7��ֱ��$\sqrt{3}$x-y-1=0����б�Ǵ�С��������
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{5��}{6}$ |