题目内容
若函数y=f(x)同时具有性质:
①是周期函数且最小正周期为π;
②在[-
,
]上是增函数;
③对任意x∈R,都有f(
-x)=f(
+x).
则函数y=f(x)的解析式可以是 (只需写出满足条件的函数y=f(x)的一个解析式即可)
①是周期函数且最小正周期为π;
②在[-
| π |
| 6 |
| π |
| 3 |
③对任意x∈R,都有f(
| π |
| 3 |
| π |
| 3 |
则函数y=f(x)的解析式可以是
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据函数的性质,进行求解即可.
解答:
解:函数y=sin(2x-
)周期为π,满足①,当x=
时,y=sin(2×
-
)=sin
为最大值,此时满足条件③,
在[-
,
]上是增函数,满足条件②,
故f(x)=sin(2x-
),满足条件,
故答案为:
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
在[-
| π |
| 6 |
| π |
| 3 |
故f(x)=sin(2x-
| π |
| 6 |
故答案为:
点评:本题考查三角函数的基本性质,单调性,对称性,周期,考查计算能力,逻辑推理能力,掌握基本函数的性质是解好题目的关键.

练习册系列答案
相关题目
已知3+sin2β+2t>(2
+
t)sin(β+
)+
对于β∈[0,
]恒成立,则t的取值范围是( )
| 2 |
| 2 |
| π |
| 4 |
2
| ||
cos(
|
| π |
| 2 |
| A、t>4 | B、t>3 |
| C、t>2 | D、t≥-2 |
已知双曲线
-
=1两个焦点为分别为F1,F2,过点F2的直线l与该双曲线的右支交于M,N两点,且△F1MN是以N为直角顶点的等腰直角三角形,则S△F1NM为( )
| x2 |
| 3 |
| y2 |
| b2 |
A、18
| ||
B、12
| ||
| C、18 | ||
| D、12 |
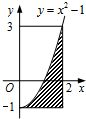 如图,设区域D={(x,y)|0≤x≤2,-1≤y≤3},向区域D内任投一点,记此点落在阴影区域M={(x,y)|0≤x≤2,-1≤y≤x2-1}的概率为p,则a=p是函数y=ax2+2x+1有两个零点的( )
如图,设区域D={(x,y)|0≤x≤2,-1≤y≤3},向区域D内任投一点,记此点落在阴影区域M={(x,y)|0≤x≤2,-1≤y≤x2-1}的概率为p,则a=p是函数y=ax2+2x+1有两个零点的( )| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
已知函数f(x)=sinωx+cosωx(ω>0),如果存在实数x1,使得对任意的实数x,都有f(x1)≤f(x)≤f(x1+2015)成立,则ω的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知tan(α+β)=1,tan(α-
)=
,则tan(β+
)的值为( )
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|