题目内容
已知函数f(x)=sinωx+cosωx(ω>0),如果存在实数x1,使得对任意的实数x,都有f(x1)≤f(x)≤f(x1+2015)成立,则ω的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两角和与差的正弦函数,正弦函数的图象
专题:计算题,三角函数的图像与性质
分析:由题意可得区间[x1,x1+2015]能够包含函数的至少一个完整的单调区间,利用两角和的正弦公式求得f(x)=
sin(ωx+
),由2015≥
•
求得ω的最小值.
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 2π |
| ω |
解答:
解:显然要使结论成立,只需保证区间[x1,x1+2015]能够包含函数的至少一个完整的单调区间即可,
又∵f(x)=sinωx+cosωx=
sin(ωx+
),则2015≥
•
,
∴ω≥
,
则ω的最小值为:
,
故选:B.
又∵f(x)=sinωx+cosωx=
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 2π |
| ω |
∴ω≥
| π |
| 2015 |
则ω的最小值为:
| π |
| 2015 |
故选:B.
点评:本题主要考查两角和的正弦公式,正弦函数的单调性和周期性,属于中档题.

练习册系列答案
相关题目
用二分法求函数f(x)=x2+3x-1的近似零点时,现经过计算知f(0)<0,f(0.5)>0,由此可得其中一个零点x0∈△,下一步应判断△的符号,以上△上依次应填的内容为( )
| A、(0,1),f(1) |
| B、(0,0.5),f(0.25) |
| C、(0.5,1),f(0.75) |
| D、(0,0.5),f(0.125) |
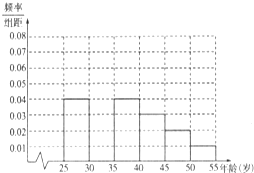 某移动公司对[25,55]岁的人群随机抽取n人进行了一次是否愿意使用4G网络的社会 调查,若愿意使用的称为“4G族”,否则称为“非4G族”,得如下统计表和各年龄段人数频率分布直方图:
某移动公司对[25,55]岁的人群随机抽取n人进行了一次是否愿意使用4G网络的社会 调查,若愿意使用的称为“4G族”,否则称为“非4G族”,得如下统计表和各年龄段人数频率分布直方图: