题目内容
已知n∈N*,则数列{
}的前n项和Sn= .
| 2n-1 |
| 2n |
考点:数列的求和
专题:等差数列与等比数列
分析:直接利用错位相减法求数列的和.
解答:
解:Sn=1•
+3•
+5•
+…+(2n-1)•
①,
Sn=1•
+3•
+…+(2n-3)•
+(2n-1)•
②,
①-②得:
Sn=
+2(
+
+…+
)-(2n-1)•
=
+2•
-(2n-1)•
=
-
-(2n-1)•
.
∴Sn=3-
-(2n-1)•
=3-
.
故答案为:3-
.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2n+1 |
| 3 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Sn=3-
| 1 |
| 2n-2 |
| 1 |
| 2n |
| 2n+3 |
| 2n |
故答案为:3-
| 2n+3 |
| 2n |
点评:本题考查了错位相减法求数列的和,一个等差数列和一个等比数列积数列,常采用错位相减法求其前n项和,是中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
圆C:x2+y2-4=0被直线l:x-y+2=0截得的弦长为( )
A、2
| ||
B、
| ||
C、
| ||
D、2
|
已知函数f(x)=x2-6x+4lnx+a(x>0),若方程f(x)=0有两个不同的实根,则实数a的值为( )
| A、a=5或a=8-4ln2 |
| B、a=5或a=8+4ln2 |
| C、a=-5或a=8-4ln2 |
| D、a=5或a=8-4ln3 |
函数y=x+
的单调减区间为( )
| 4 |
| x |
| A、(-2,0)及(0,2) |
| B、(-2,0)∪(0,2) |
| C、(0,2)及(-∞,-2) |
| D、(-2,2) |
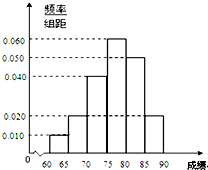 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数