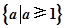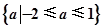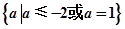题目内容
不等式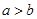 与
与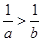 同时成立的充要条件为( )
同时成立的充要条件为( )
A.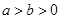 | B.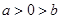 | C.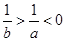 | D.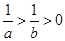 |
B
解析试题分析:∵ ,因此现要
,因此现要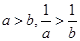 同时成立,需
同时成立,需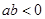
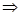
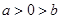 .
.
考点:作差法证明不等式.

练习册系列答案
相关题目
设函数 条件
条件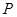 :“
:“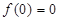 ”;条件
”;条件 :“
:“ 为奇函数”,则
为奇函数”,则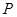 是
是 的( ).
的( ).
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
在四边形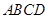 中,“
中,“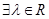 ,使得
,使得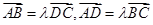 ”是“四边形
”是“四边形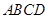 为平行四边形”的( )
为平行四边形”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知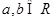 ,则
,则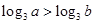 是
是  的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若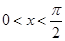 ,则“
,则“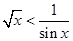 ”是“
”是“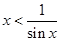 ”的( )
”的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既非充分又非必要条件 |
命题“若a>b,则2a>2b-1”的否命题为( )
| A.若a>b,则有2a≤2b-1. | B.若a≤b,则有2a≤2b-1. |
| C.若a≤b,则有2a>2b-1. | D.若2a≤2b-1,则有a≤b. |
原命题为“若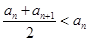 ,
,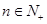 ,则
,则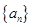 为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
| A.真,真,真 | B.假,假,真 | C.真,真,假 | D.假,假,假 |
下列说法中正确的是( )
A.命题“若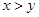 ,则 ,则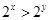 ”的否命题为假命题 ”的否命题为假命题 |
B.命题“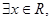 使得 使得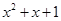 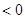 ”的否定为“ ”的否定为“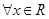 ,满足 ,满足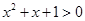 ” ” |
C.设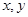 为实数,则“ 为实数,则“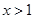 ”是“ ”是“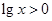 ”的充要条件 ”的充要条件 |
D.若“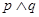 ”为假命题,则 ”为假命题,则 和 和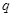 都是假命题 都是假命题 |
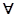 x∈[1,2],x2-a≥0”,命题q:“
x∈[1,2],x2-a≥0”,命题q:“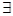 x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )