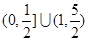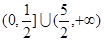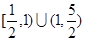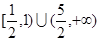题目内容
已知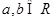 ,则
,则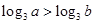 是
是  的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:因为由 ,
,
但是 ,所以,
,所以,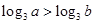 是
是  的充分不必要条件.
的充分不必要条件.
故选A.
考点:1、对数函数的性质;2、指数函数的性质;3、充要条件.

练习册系列答案
相关题目
“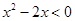 ”是“
”是“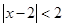 ”的( )
”的( )
| A.充分条件 | B.充分而不必要条件 |
| C.必要而不充分条件 | D.既不充分也不必要条件 |
下列说法:
(1)命题“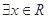 ,使得
,使得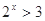 ”的否定是“
”的否定是“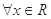 ,使得
,使得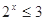 ”
”
(2)命题“函数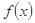 在
在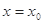 处有极值,则
处有极值,则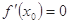 ”的否命题是真命题
”的否命题是真命题
(3)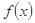 是(
是( ,0)∪(0,
,0)∪(0,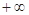 )上的奇函数,
)上的奇函数,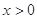 时的解析式是
时的解析式是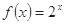 ,则
,则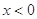 的解析式为
的解析式为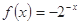
其中正确的说法的个数是( ).
| A.0个 | B.1个 | C.2个 | D.3个 |
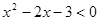 成立的一个必要不充分条件是( )
成立的一个必要不充分条件是( )
A.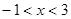 | B.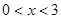 | C.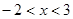 | D.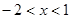 |
设 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出如下四个命题:
①若“ 且
且 ”为假命题,则
”为假命题,则 、
、 均为假命题;
均为假命题;
②命题“若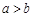 ,则
,则 ”的否命题为“若
”的否命题为“若 ,则
,则 ”;
”;
③“ ”的否定是“
”的否定是“ ”;
”;
④在△ 中,“
中,“ ”是“
”是“ ”的充要条件.
”的充要条件.
其中不正确的命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
不等式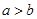 与
与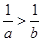 同时成立的充要条件为( )
同时成立的充要条件为( )
A.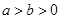 | B.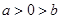 | C.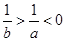 | D.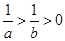 |
给出下面四个命题:
p1:?x∈(0,+∞),(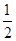 )x<(
)x<(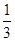 )x;
)x;
p2:?x∈(0,1),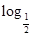 x>
x>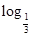 x;
x;
p3:?x∈(0,+∞),(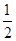 )x>
)x>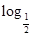 x;
x;
p4:?x∈(0,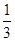 ),(
),(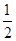 )x<
)x<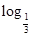 x.
x.
其中的真命题是( )
| A.p1,p3 | B.p1,p4 | C.p2,p3 | D.p2,p4 |
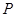 :函数
:函数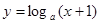 在
在 内单调递减;
内单调递减;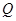 :曲线
:曲线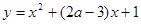 与
与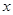 轴没有交点.如果“
轴没有交点.如果“ 的取值范围是( )
的取值范围是( )