题目内容
设函数 条件
条件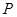 :“
:“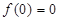 ”;条件
”;条件 :“
:“ 为奇函数”,则
为奇函数”,则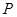 是
是 的( ).
的( ).
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
B.
解析试题分析:“充分性”:当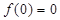 ,有
,有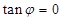 ,得
,得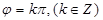 ,则
,则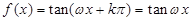 ,此函数满足
,此函数满足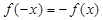 可知为奇函数,所以充分性成立;“必要性:”当
可知为奇函数,所以充分性成立;“必要性:”当 为奇函数时,有
为奇函数时,有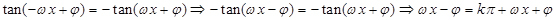
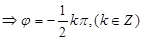 ,此时
,此时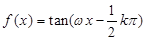 ,当
,当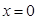 时,
时,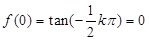 或
或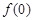 不存在,所以必要性不成立.综上所述,
不存在,所以必要性不成立.综上所述,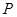 是
是 的充分不必要条件.
的充分不必要条件.
考点:充要条件的判定,奇函数的定义,正切函数的性质.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
“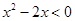 ”是“
”是“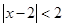 ”的( )
”的( )
| A.充分条件 | B.充分而不必要条件 |
| C.必要而不充分条件 | D.既不充分也不必要条件 |
.2x2-5x-3<0的一个必要不充分条件是
A.-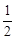 <x<3 <x<3 | B.-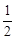 <x<0 <x<0 |
C.-3<x<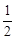 | D.-1<x<6 |
以下有关命题的说法错误的是( )
A.命题“若 则x=1”的逆否命题为“若 则x=1”的逆否命题为“若 ” ” |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C.若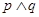 为假命题,则p、q均为假命题 为假命题,则p、q均为假命题 |
D.对于命题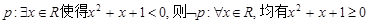 |
下列命题中,真命题的个数有( )
①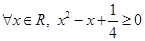 ;
;
②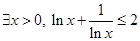 ;
;
③“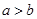 ”是“
”是“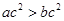 ”的充要条件;
”的充要条件;
④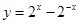 是奇函数.
是奇函数.
| A.1个 | B.2个 | C.3个 | D.4个 |
下列说法:
(1)命题“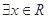 ,使得
,使得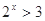 ”的否定是“
”的否定是“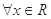 ,使得
,使得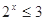 ”
”
(2)命题“函数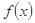 在
在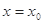 处有极值,则
处有极值,则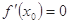 ”的否命题是真命题
”的否命题是真命题
(3)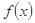 是(
是( ,0)∪(0,
,0)∪(0,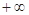 )上的奇函数,
)上的奇函数,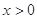 时的解析式是
时的解析式是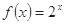 ,则
,则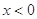 的解析式为
的解析式为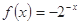
其中正确的说法的个数是( ).
| A.0个 | B.1个 | C.2个 | D.3个 |
不等式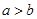 与
与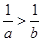 同时成立的充要条件为( )
同时成立的充要条件为( )
A.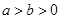 | B.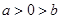 | C.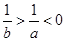 | D.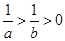 |
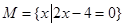 ,集合
,集合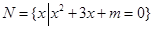
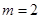 时,求
时,求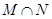 ,
,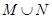
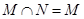 ,求集合
,求集合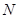
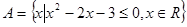 ; B=
; B=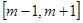 ,
,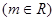
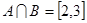 ,求实数
,求实数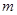 的值;
的值;