题目内容
在四边形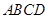 中,“
中,“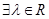 ,使得
,使得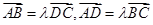 ”是“四边形
”是“四边形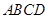 为平行四边形”的( )
为平行四边形”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
C.
解析试题分析:若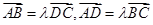 :则
:则 四边形
四边形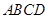 是平行四边形;
是平行四边形;
若四边形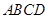 是平行四边形:则
是平行四边形:则 ,即存在
,即存在 ,满足
,满足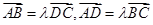 ,因此是充分必要条件.
,因此是充分必要条件.
考点:1.充分必要条件;2.平面向量共线的表示.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
下列命题中,真命题的个数有( )
①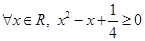 ;
;
②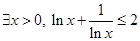 ;
;
③“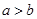 ”是“
”是“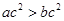 ”的充要条件;
”的充要条件;
④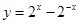 是奇函数.
是奇函数.
| A.1个 | B.2个 | C.3个 | D.4个 |
下列说法:
(1)命题“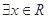 ,使得
,使得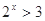 ”的否定是“
”的否定是“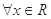 ,使得
,使得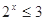 ”
”
(2)命题“函数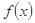 在
在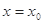 处有极值,则
处有极值,则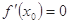 ”的否命题是真命题
”的否命题是真命题
(3)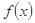 是(
是( ,0)∪(0,
,0)∪(0,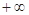 )上的奇函数,
)上的奇函数,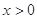 时的解析式是
时的解析式是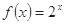 ,则
,则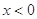 的解析式为
的解析式为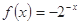
其中正确的说法的个数是( ).
| A.0个 | B.1个 | C.2个 | D.3个 |
已知命题p: ,
, .则
.则 为
为
A. , , | B. , , |
C. , , | D. , , |
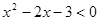 成立的一个必要不充分条件是( )
成立的一个必要不充分条件是( )
A.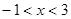 | B.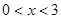 | C.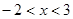 | D.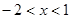 |
设 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
不等式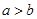 与
与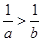 同时成立的充要条件为( )
同时成立的充要条件为( )
A.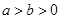 | B.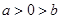 | C.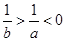 | D.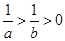 |
设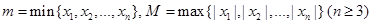 ,其中
,其中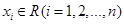 .那么“
.那么“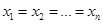 ”是“
”是“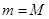 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.非充分非必要条件 |
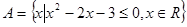 ; B=
; B=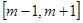 ,
,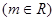
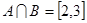 ,求实数
,求实数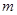 的值;
的值;