题目内容
已知函数f(x)=sin(πx+
),x∈R,以下结论:
①函数f(x)的最小正周期是2;
②函数f(x)的图象关于点(-
,0)对称;
③函数f(x)的图象关于直线x=-
对称;
④函数f(x)在区间(0,
)上是增函数;
⑤函数f(x)的图象可由函数y=sinπx的图象向左平移
得到.
其中正确的序号是 .
| π |
| 3 |
①函数f(x)的最小正周期是2;
②函数f(x)的图象关于点(-
| 1 |
| 3 |
③函数f(x)的图象关于直线x=-
| 5 |
| 6 |
④函数f(x)在区间(0,
| 1 |
| 3 |
⑤函数f(x)的图象可由函数y=sinπx的图象向左平移
| π |
| 3 |
其中正确的序号是
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由条件利用y=Asin(ωx+φ)的图象和性质,判断各个选项是否正确,从而得出结论.
解答:
解:对于函数f(x)=sin(πx+
),x∈R,
它的周期为
=2,故①正确.
令x=-
,求得f(x)=0,故f(x)的图象关于点(-
,0)对称,故②正确.
令x=-
,求得f(x)=-1,是函数的最小值,故f(x)的图象关于直线x=-
对称,故③正确.
令2kπ-
≤πx+
≤2kπ+
,k∈z,求得2k-
≤x≤2k+
,
故函数的增区间为[2k-
,2k+
],k∈z,故④不正确.
把函数y=sinπx的图象向左平移
,可得函数y=sinπ(x-
)=sin(πx-
)的图象,故⑤不正确,
故答案为:①②③.
| π |
| 3 |
它的周期为
| 2π |
| π |
令x=-
| 1 |
| 3 |
| 1 |
| 3 |
令x=-
| 5 |
| 6 |
| 5 |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5 |
| 6 |
| 1 |
| 6 |
故函数的增区间为[2k-
| 5 |
| 6 |
| 1 |
| 6 |
把函数y=sinπx的图象向左平移
| π |
| 3 |
| π |
| 3 |
| π2 |
| 3 |
故答案为:①②③.
点评:本题主要考查y=Asin(ωx+φ)的图象和性质,属于基础题.

练习册系列答案
相关题目
将一枚骰子抛掷两次,若先后出现的点数分别为x、y,则满足x=2y的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
对“a、b、c至少有一个是正数”的反设是( )
| A、a、b、c至少有一个是负数 |
| B、a、b、c至少有一个是非正数 |
| C、a、b、c都是非正数 |
| D、a、b、c都是正数 |
已知x,y∈R+,且xy2=8,则4x+y的最小值为( )
A、4
| ||
B、6
| ||
| C、6 | ||
| D、2 |
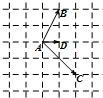 已知向量
已知向量| AC |
| AD |
| AB |
| AC |
| AB |
| AD |
| A、2 | B、-2 | C、3 | D、-3 |
 对一块边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=
对一块边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=