题目内容
10．设x＞2，则$y=x+\frac{4}{x-2}$的最小值是6．分析 变形利用基本不等式的性质即可得出．
解答 解：∵x＞2，则x-2＞0，
∴$y=x+\frac{4}{x-2}$=x-2+$\frac{4}{x-2}$+2$≥2\sqrt{（x-2）•\frac{4}{x-2}}$+2=6，当且仅当x=4时取等号．
因此y的最小值是6．
故答案为：6．
点评 本题考查了基本不等式的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
18．已知函数f（x）=ax2+2ax+4（-3＜a＜0），其图象上两点的横坐标为x1、x&2满足x1＜x2，且x1+x2=1+a，则由（ ）
| A． | f（x1）＜f（x2） | B． | f（x1）=f（x2） | ||
| C． | f（x1）＞f（x2） | D． | f（x1）、f（x&2）的大小不确定 |
15．判断函数f（x）=$\frac{{\sqrt{{x^2}+1}+x-1}}{{\sqrt{{x^2}+1}+x+1}}$的奇偶性（ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 非奇非偶函数 |
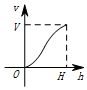
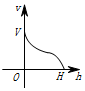
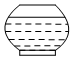一个高为H，容积为V的鱼缸的轴截面如图所示，向鱼缸里注水，若鱼缸里的水面高度为h时，鱼缸里的水的体积为V'，则函数V'=f（h）的大致图象可能是（ ）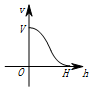
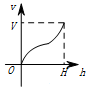
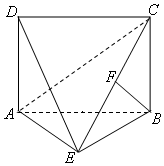如图，四边形ABCD为矩形，DA⊥平面ABE，AE=EB=BC=2，BF⊥平面ACE于点F，且点F在CE上．