题目内容
已知函数f(x)=loga
.
(1)判断函数f(x)在(1,+∞)上的单调性;并给予证明.
(2)令函数g(x)=-ax2+8(x-1)af(x)-5,a≥8时,存在最大实数t,使得x∈(1,t],-5≤g(x)≤5恒成立,试写出t与a的关系式,并求出最大实数t.
| 1+x |
| x-1 |
(1)判断函数f(x)在(1,+∞)上的单调性;并给予证明.
(2)令函数g(x)=-ax2+8(x-1)af(x)-5,a≥8时,存在最大实数t,使得x∈(1,t],-5≤g(x)≤5恒成立,试写出t与a的关系式,并求出最大实数t.
考点:对数函数图象与性质的综合应用,函数单调性的判断与证明,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)令t=
=1+
,显然函数t在(1,+∞)上的单调递减,讨论当a的范围,可得函数f(x)=loga t在(1,+∞)上的单调性.
(2)由题意可得函数g(x)=-a(x-
)2+3+
的对称轴为x=
,且
∈(0,
],故f(x)在(1,t]上是减函数,故g(t)<g(x)≤g(1),由g(1)=11-a≤3<5,结合题意可得g(t)=-5,化简可得t与a的关系式,再根据 a=
≥8,求得t的最大值.
| 1+x |
| x-1 |
| 2 |
| x-1 |
(2)由题意可得函数g(x)=-a(x-
| 4 |
| a |
| 16 |
| a |
| 4 |
| a |
| 4 |
| a |
| 1 |
| 2 |
| 8t+8 |
| t2 |
解答:
解:(1)令t=
=1+
,显然函数t在(1,+∞)上的单调递减,
故当a>1时,函数f(x)=loga t在(1,+∞)上的单调递减,
当0<a<1时,函数f(x)=loga t在(1,+∞)上的单调递增.
(2)∵f(x)=loga
,∴af(x)=
,
∴函数g(x)=-ax2+8(x-1)af(x)-5=-ax2+8(x+1)-5=-a(x-
)2+3+
的对称轴为x=
,
∵a≥8时,∴
∈(0,
],故f(x)在(1,t]上是减函数,故g(t)<g(x)≤g(1).
g(1)=11-a≤3<5,
∵存在最大实数t,使得x∈(1,t],-5≤g(x)≤5恒成立,∴g(t)=-at2+8t+3=-5,
化简可得 at2-8t-8=0,即 a=
.
再根据 a=
≥8,求得
≤t≤
,故 tmax=
.
| 1+x |
| x-1 |
| 2 |
| x-1 |
故当a>1时,函数f(x)=loga t在(1,+∞)上的单调递减,
当0<a<1时,函数f(x)=loga t在(1,+∞)上的单调递增.
(2)∵f(x)=loga
| 1+x |
| x-1 |
| x+1 |
| x-1 |
∴函数g(x)=-ax2+8(x-1)af(x)-5=-ax2+8(x+1)-5=-a(x-
| 4 |
| a |
| 16 |
| a |
| 4 |
| a |
∵a≥8时,∴
| 4 |
| a |
| 1 |
| 2 |
g(1)=11-a≤3<5,
∵存在最大实数t,使得x∈(1,t],-5≤g(x)≤5恒成立,∴g(t)=-at2+8t+3=-5,
化简可得 at2-8t-8=0,即 a=
| 8t+8 |
| t2 |
再根据 a=
| 8t+8 |
| t2 |
1-
| ||
| 2 |
1+
| ||
| 2 |
1+
| ||
| 2 |
点评:本题主要考查对数函数的图象和性质综合应用,二次函数的性质,函数的最值及其几何意义,属于中档题.

练习册系列答案
相关题目


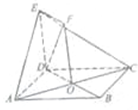 如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=
如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=