题目内容
5.在冬奥会志愿者活动中,甲、乙等5人报名参加了A,B,C三个项目的志愿者工作,因工作需要,每个项目仅需1名志愿者,且甲不能参加A,B项目,乙不能参加B,C项目,那么共有21种不同的志愿者分配方案.(用数字作答)分析 由题意可以分为四类,根据分类计数原理可得.
解答 解:若甲,乙都参加,则甲只能参加C项目,乙只能参见A项目,B项目有3种方法,
若甲参加,乙不参加,则甲只能参加C项目,A,B项目,有A32=6种方法,
若甲参加,乙不参加,则乙只能参加A项目,B,C项目,有A32=6种方法,
若甲不参加,乙不参加,有A33=6种方法,
根据分类计数原理,共有3+6+6+6=21种.
点评 本题考查了分类计数原理,关键是分类,属于中档题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
20.设集合A={x|x2+4x<0},集合B={n|n=2k-1,k∈Z},则A∩B=( )
| A. | {-1,1} | B. | {1,3} | C. | {-3,-1} | D. | {-3,-1,1,3} |
10.为了解一批灯泡(共5000只)的使用寿命,从中随机抽取了100只进行测试,其使用寿命(单位:h)如表:
根据该样本的频数分布,估计该批灯泡使用寿命不低于1100h的灯泡只数是1400.
| 使用寿命 | [500,700) | [700,900) | [900,1100) | [1100,1300) | [1300,1500] |
| 只数 | 5 | 23 | 44 | 25 | 3 |
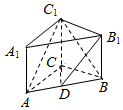 如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.
如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.