Question

13．在△ABC中，∠BAC=60°，AB=5，AC=4，D是AB上一点，且$\overrightarrow{AB}$•$\overrightarrow{CD}$=5，则|$\overrightarrow{BD}$|等于（　　）

• A． 2
• B． 4
• C． 6
• D． 1

Answer 1

分析 依题意，作出图形，设$\overrightarrow{AD}$=k$\overrightarrow{AB}$，利用三角形法则可知$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\overrightarrow{AD}$=-$\overrightarrow{AC}$+k$\overrightarrow{AB}$，再由$\overrightarrow{AB}$•$\overrightarrow{CD}$=5可求得k，从而可求得|$\overrightarrow{BD}$|的值．

解答 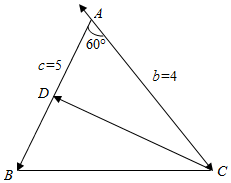解：∵在△ABC中，∠BAC=60°，AB=5，AC=4，D是AB上一点，且$\overrightarrow{AB}$•$\overrightarrow{CD}$=5，
作图如下：

设$\overrightarrow{AD}$=k$\overrightarrow{AB}$，
∵$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\overrightarrow{AD}$=-$\overrightarrow{AC}$+k$\overrightarrow{AB}$，
∴$\overrightarrow{AB}$•$\overrightarrow{CD}$=$\overrightarrow{AB}$•（-$\overrightarrow{AC}$+k$\overrightarrow{AB}$）=-|$\overrightarrow{AB}$||$\overrightarrow{AC}$|cos60°+k${\overrightarrow{AB}}^{2}$=-5×4×$\frac{1}{2}$+25k=5，
解得：k=$\frac{3}{5}$，
∴|$\overrightarrow{AD}$|=5×$\frac{3}{5}$=3，
∴|$\overrightarrow{BD}$|=5-3=2．
故选：A．

点评 本题考查平面向量数量积的运算，考查平面向量的加法运算（三角形法则）及平面向量共线基本定理的应用，考查数形结合思想，属于中档题．