题目内容
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b),从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为t,在区间[1,
]和[2,4]分别各取一个数,记为m和n,则方程
+
=1表示焦点在x轴上的椭圆的概率是( )
| α |
| t |
| 3 |
| x2 |
| m2 |
| y2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:椭圆的简单性质,古典概型及其概率计算公式
专题:计算题,圆锥曲线的定义、性质与方程,概率与统计
分析:本题是一个古典概型,a的取法有2中,b的取法有3中,得到可以组成向量的个数,从中任取两个向量共C62种取法,再确定平面区域及相应的面积,根据概率公式得到结果.
解答:
 解:由题意知本题是一个古典概型,试验发生包含的事件是取出数字,构成向量,a的取法有2种,b的取法有3种,故向量
解:由题意知本题是一个古典概型,试验发生包含的事件是取出数字,构成向量,a的取法有2种,b的取法有3种,故向量
有6个,从中任取两个向量共C62=15种取法,即t=15;
∴区间[1,5]和[2,4]围成一个矩形,面积为8,
其中满足m>n的区域如图所示,面积为
=4,
∴方程
+
=1表示焦点在x轴上的椭圆的概率是
=
.
故选:D.
 解:由题意知本题是一个古典概型,试验发生包含的事件是取出数字,构成向量,a的取法有2种,b的取法有3种,故向量
解:由题意知本题是一个古典概型,试验发生包含的事件是取出数字,构成向量,a的取法有2种,b的取法有3种,故向量| α |
∴区间[1,5]和[2,4]围成一个矩形,面积为8,
其中满足m>n的区域如图所示,面积为
| (1+3)×2 |
| 2 |
∴方程
| x2 |
| m2 |
| y2 |
| n2 |
| 4 |
| 8 |
| 1 |
| 2 |
故选:D.
点评:本题考查古典概型及其概率计算公式,考查组合数问题、考查平面区域及面积的计算,综合性强.

练习册系列答案
相关题目
利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X和Y有关系”的可信度.如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为( )
| P(k2>k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
| A、25% | B、75% |
| C、2.5% | D、97.5% |
cos22°cos38°-sin22°sin38°的值是( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若梯形的中位线被它的两条对角线三等分,则梯形的上底a与下底b(a<b)的比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
把二进制的数101111(2)化成十进制的数是( )
| A、47 | B、56 | C、122 | D、64 |
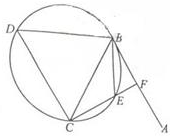 如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.