题目内容
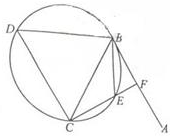 如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.(Ⅰ)证明:DB=DC;
(Ⅱ)设圆的半径为1,BC=
| 3 |
考点:圆的切线的性质定理的证明
专题:立体几何
分析:(I)如图所示,连接DE.由于DB垂直BE交圆于点D,可得∠DBE=90°.即DE为圆的直径.由于∠ABC的角平分线BE交圆于点E,利用同圆中的弧圆周角弦之间的关系可得∠DCB=∠DBC,DB=DC.
(II)由(I)利用垂径定理及其推论可得:DE⊥BC,且平分BC,设中点为M,外接圆的圆心为点O.连接OB,OC,可得OB⊥AB.在Rt△BOM中,可得∠OBM=30°,∠BOE=60°.进而得到∠CBA=60°.∠BCE=30°,∠BFC=90°.即可得到△BCF外接圆的半径=
BC.
(II)由(I)利用垂径定理及其推论可得:DE⊥BC,且平分BC,设中点为M,外接圆的圆心为点O.连接OB,OC,可得OB⊥AB.在Rt△BOM中,可得∠OBM=30°,∠BOE=60°.进而得到∠CBA=60°.∠BCE=30°,∠BFC=90°.即可得到△BCF外接圆的半径=
| 1 |
| 2 |
解答:
(I)证明:如图所示,连接DE.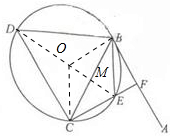
∵DB垂直BE交圆于点D,∴∠DBE=90°.
∴DE为圆的直径.
∵∠ABC的角平分线BE交圆于点E,
∴
=
,
∴
=
,
∴∠DCB=∠DBC,
∴DB=DC.
(II)解:由(I)可知:DE⊥BC,且平分BC,设中点为M,外接圆的圆心为点O.
连接OB,OC,则OB⊥AB.
在Rt△BOM中,OB=1,BM=
BC=
.
∴∠OBM=30°,∠BOE=60°.
∴∠CBA=60°.
∴∠BCE=
∠BOE=30°.
∴∠BFC=90°.
∴△BCF外接圆的半径=
BC=
.

∵DB垂直BE交圆于点D,∴∠DBE=90°.
∴DE为圆的直径.
∵∠ABC的角平分线BE交圆于点E,
∴
 |
| BE |
 |
| CE |
∴
 |
| DB |
 |
| DC |
∴∠DCB=∠DBC,
∴DB=DC.
(II)解:由(I)可知:DE⊥BC,且平分BC,设中点为M,外接圆的圆心为点O.
连接OB,OC,则OB⊥AB.
在Rt△BOM中,OB=1,BM=
| 1 |
| 2 |
| ||
| 2 |
∴∠OBM=30°,∠BOE=60°.
∴∠CBA=60°.
∴∠BCE=
| 1 |
| 2 |
∴∠BFC=90°.
∴△BCF外接圆的半径=
| 1 |
| 2 |
| ||
| 2 |
点评:本题综合考查了圆的切线的性质、同圆中的弧圆周角弦之间的关系、垂径定理及其推论、直角三角形外接圆的性质等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=sinx-
x(x∈[0,π]),那么下列结论正确的是( )
| 1 |
| 2 |
A、f(x)在[0,
| ||
B、f(x)在[
| ||
C、?x∈[0,π],f(x)≤f(
| ||
D、?x∈[0,π],f(x)>f(
|