题目内容
17.已知函数y=f(x),x∈D,若存在常数C,对任意x1∈D,存在唯一的x2∈D,使得$\sqrt{f({x_1})•f({x_2})}=C$,则称常数C是函数f(x)在D上的“湖中平均数”.若已知函数$f(x)={({\frac{1}{2}})^x},x∈[{0,2016}]$,则f(x)在[0,2016]上的“湖中平均数”是$(\frac{1}{2})^{1008}$.分析 根据已知中函数y=f(x),x∈D,若存在常数C,对?x1∈D,?唯一的x2∈D,使得$\sqrt{f({x_1})•f({x_2})}=C$,则称常数C是函数f(x)在D上的“湖中平均数”.根据函数f(x)=($\frac{1}{2}$)x,x∈[0,2016],为单调减函数,可得f(x)在[0,2016]上的“湖中平均数”是其最大值和最小值的几何平均数
解答 解:由已知中湖中平均数的定义可得C即为函数y=f(x),x∈D最大值与最小值的几何平均数
又∵函数f(x)=($\frac{1}{2}$)x,x∈[0,2016]为减函数
故其最大值M=1,最小值m=($\frac{1}{2}$)2016
故C=$\sqrt{(\frac{1}{2})^{2016}}$=$(\frac{1}{2})^{1008}$;
故答案为:${(\frac{1}{2})^{1008}}$
点评 本题考查的知识点是函数单调性的性质,其中根据已知判断出C等于函数在区间D上最大值与最小值的几何平均数,是解答本题的关键.

练习册系列答案
相关题目
8.如图所示的流程图的功能是( )
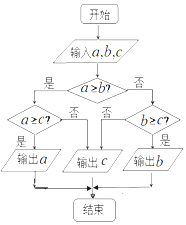

| A. | 输出a,b,c的最大值 | B. | 输出a,b,c的最小值 | ||
| C. | 将a,b,c从大到小排列 | D. | 将a,b,c从小到大排列 |
5.从2 012名学生中选取50名学生参加数学竞赛,若采用下面的方法选取:先用简单随机抽样从2 012人中剔除12人,剩下的2 000人再按系统抽样的方法抽取50人,则在2 012人中,每人入选的概率( )
| A. | 不全相等 | B. | 均不相等 | ||
| C. | 都相等,且为$\frac{1}{40}$ | D. | 都相等,且为$\frac{25}{1006}$ |
9. 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中:
①|BM|是定值;
②点M在圆上运动;
③一定存在某个位置,使DE⊥A1C;
④一定存在某个位置,使MB∥平面A1DE.
其中正确的命题是( )
 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中:①|BM|是定值;
②点M在圆上运动;
③一定存在某个位置,使DE⊥A1C;
④一定存在某个位置,使MB∥平面A1DE.
其中正确的命题是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
6.用五点作图法作y=2sin4x的图象时,首先描出的五个点的横坐标是( )
| A. | 0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π | B. | 0,$\frac{π}{4}$,$\frac{π}{2}$,$\frac{3π}{4}$,π | C. | 0,$\frac{π}{8}$,$\frac{π}{4}$,$\frac{3π}{8}$,$\frac{π}{2}$ | D. | 0,$\frac{π}{6}$,$\frac{π}{3}$,$\frac{3π}{2}$,$\frac{2}{3}$π |