题目内容
9.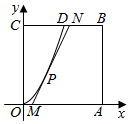 某地要建造一个边长为2(单位:km)的正方形市民休闲公园OABC,将其中的区域ODC开挖成一个池塘,如图建立平面直角坐标系后,点D的坐标为(1,2),曲线OD是函数y=ax2图象的一部分,对边OA上一点M在区域OABD内作一次函数y=kx+b(k>0)的图象,与线段DB交于点N(点N不与点D重合),且线段MN与曲线OD有且只有一个公共点P,四边形MABN为绿化风景区:
某地要建造一个边长为2(单位:km)的正方形市民休闲公园OABC,将其中的区域ODC开挖成一个池塘,如图建立平面直角坐标系后,点D的坐标为(1,2),曲线OD是函数y=ax2图象的一部分,对边OA上一点M在区域OABD内作一次函数y=kx+b(k>0)的图象,与线段DB交于点N(点N不与点D重合),且线段MN与曲线OD有且只有一个公共点P,四边形MABN为绿化风景区:(1)求证:b=-$\frac{{k}^{2}}{8}$;
(2)设点P的横坐标为t,①用t表示M、N两点坐标;②将四边形MABN的面积S表示成关于t的函数S=S(t),并求S的最大值.
分析 (1)根据函数y=ax2过点D,求出解析式y=2x2;
由$\left\{\begin{array}{l}{y=kx+b}\\{y={2x}^{2}}\end{array}\right.$消去y,利用△=0证明结论成立;
(2)①写出点P的坐标(t,2t2),代入直线MN的方程,用t表示出直线方程,
利用直线方程求出M、N的坐标;
②将四边形MABN的面积S表示成关于t的函数S(t),
利用基本不等式即可求出S的最大值.
解答 (1)证明:函数y=ax2过点D(1,2),
代入计算得a=2,
∴y=2x2;
由$\left\{\begin{array}{l}{y=kx+b}\\{y={2x}^{2}}\end{array}\right.$,消去y得2x2-kx-b=0,
由线段MN与曲线OD有且只有一个公共点P,
得△=(-k)2-4×2×b=0,
解得b=-$\frac{{k}^{2}}{8}$;
(2)解:设点P的横坐标为t,则0<t<1,
∴点P(t,2t2);
①直线MN的方程为y=kx+b,
即y=kx-$\frac{{k}^{2}}{8}$过点P,
∴kt-$\frac{{k}^{2}}{8}$=2t2,
解得k=4t;
y=4tx-2t2
令y=0,解得x=$\frac{t}{2}$,∴M($\frac{t}{2}$,0);
令y=2,解得x=$\frac{t}{2}$+$\frac{1}{2t}$,∴N($\frac{t}{2}$+$\frac{1}{2t}$,2);
②将四边形MABN的面积S表示成关于t的函数为
S=S(t)=2×2-$\frac{1}{2}$×2×[$\frac{t}{2}$+($\frac{t}{2}$+$\frac{1}{2t}$)]=4-(t+$\frac{1}{2t}$),其中0<t<1;
由t+$\frac{1}{2t}$≥2•$\sqrt{t•\frac{1}{2t}}$=$\sqrt{2}$,当且仅当t=$\frac{1}{2t}$,即t=$\frac{\sqrt{2}}{2}$时“=”成立,
所以S≤4-$\sqrt{2}$;即S的最大值是4-$\sqrt{2}$.
点评 本题考查了函数模型的应用问题,也考查了阅读理解能力,是综合性题目.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{4}$ |
| A. | ac<bc | B. | abc<bac | C. | ca<cb | D. | logac<logbc |
| A. | -1 | B. | 1 | C. | 1或-1 | D. | 2 |
| A. | 2 | B. | $\frac{4}{3}$ | C. | $-\frac{3}{2}$ | D. | 4 |
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | -3 |
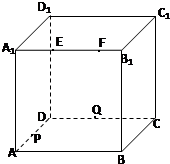 如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:
如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论: