题目内容
13.求证:函数f(x)=$\frac{x+a}{x+1}$(a>1)在区间(-1,+∞)上是减函数.分析 根据函数单调性的定义证明即可.
解答 解:设?x1,x2∈(-1,+∞)且x1<x2,
则f(x1)-f(x2)=$\frac{{x}_{1}+a}{{x}_{1}+1}$-$\frac{{x}_{2}+a}{{x}_{2}+1}$=$\frac{(1-a){(x}_{1}{-x}_{2})}{{(x}_{1}+1){(x}_{2}+1)}$,
∵${x_1},{x_2}∈(-1,+∞),且{x_1}<{x_2}\\$,
∴${x_1}+1>0,{x_2}+1>0,{x_1}-{x_2}<0\\ \begin{array}{l}{又}&{\;}\end{array}a>1\\$,
∴$1-a<0\\$,
∴$\frac{{(1-a)({x_1}-{x_2})}}{{({x_1}+1)({x_2}+1)}}>0,即f({x_1})-f({x_2})>0\\$,
∴$f({x_1})>f({x_2})\\,故函数f(x)在区间(-1,+∞)是减函数.\end{array}$.
点评 本题考查了函数单调性的定义,是一道基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
4.若$\overline z$=$\frac{i}{1+i}$,则z•$\overline z$=( )
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
1.已知A={(x,y)|y=x-3},B={(x,y)|y=-x-5},则A∩B为( )
| A. | {-1,4} | B. | {-1,-4} | C. | {(-1,4)} | D. | {(-1,-4)} |
8.已知函数f(x)=$\left\{\begin{array}{l}x-2,\;x≥0\\{2^x},\;x<0\end{array}$,则f(-1)=( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | -3 |
2.命题p:“?x≥0,e${\;}^{{x}_{0}}$<x0+1”,则¬p是( )
| A. | ?x≥0,ex<x+1 | B. | ?x≥0,ex>x+1 | C. | ?x≥0,ex≥x+1 | D. | ?x≥0,ex≥x+1 |
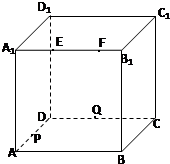 如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:
如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论: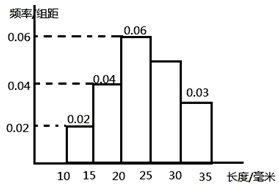 对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;
对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;