Question

四边形ABCD中，B=C=120°，AB=4，BC=CD=2，求该四边形的面积等于多少．

Answer 1

考点：正弦定理

专题：解三角形

分析：连接BD，在△BCD中利用BC=CD∠BCD=120°求得BD，进而利用三角形面积公式求得三角形BCD的面积．在△ABD中，依题意求得∠ABD=90°进而利用两直角边求得三角形的面积，最后相加即可．

解答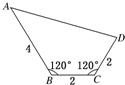： 解：连接BD，在△BCD中，BC=CD=2，∠BCD=120°，故△BCD为等腰三角形，
∴∠CBD=30°，BD=2

3

，S_△BCD=

1

2

×2×2×sin120°=

3

，
在△ABD中，∠ABD=120°-30°=90°，AB=4，BD=2

3

，
∴S_△ABD=

1

2

AB•BD=

1

2

×4×2

3

=4

3

，
∴四边形ABCD的面积是5

3

．

点评：本题主要考查了解三角形问题，考查了三角函数基础知识的综合应用，利用分割法求多边形的面积，体现了转化、数形结合的数学思想，属于基础题．