题目内容
设集合A={-2，0，3，4}，B={x|x2-2x-3=0}，则A∩B=（ ）
| A、{0} | B、{3} |
| C、{0，2} | D、{0，2，4} |
考点：交集及其运算
专题：集合
分析：利用交集定义求解．
解答：
解：∵集合A={-2，0，3，4}，B={x|x2-2x-3=0}={-1，3}，
∴A∩B={3}．
故选：B．
∴A∩B={3}．
故选：B．
点评：本题考查交集的求法，解题时要认真审题，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
x=（a+3）（a-5）与y=（a+2）（a-4）的大小关系是（ ）
| A、x＞y | B、x=y |
| C、x＜y | D、不能确定 |
下列命题中为真命题的是（ ）
| A、若数列{an}为等比数列的充要条件是an2=an-1•an+1 |
| B、“a=1是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件 |
| C、若命题p：“?x∈R，x2-x-1＞0”，则命题的否定为：“?x∈R，x2-x-1≤0” |
| D、直线a，b为异面直线的充要条件是直线a，b不相交 |
-401是等差数列-5，-9，-13…的第（ ）项．
| A、98 | B、99 |
| C、100 | D、101 |
方程2x+x=5的根所在的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
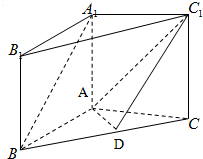在三棱柱A1B1C1-ABC中，A1A⊥平面ABC，A1A=AB=AC=2，BC=2