题目内容
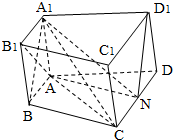 如图,在侧棱与底面垂直的四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥BC,且A1A=AB=BC=1,CD=2.
如图,在侧棱与底面垂直的四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥BC,且A1A=AB=BC=1,CD=2.(1)求证:AB1⊥平面A1BC;
(2)在线段CD上是否存在点N,使得D1N∥平面A1BC?若存在,求出此时三棱锥N-AA1C的体积;若不存在,请说明理由.
考点:直线与平面垂直的判定,直线与平面平行的性质
专题:空间位置关系与距离
分析:(1)易证明BC⊥AB1,AB1⊥A1B,故AB1⊥平面A1BC;
(2)存在点N,取CD的中点N,易证平行四边形ABCN为正方形和D1N∥A1B,D1N∥平面A1BC,求三棱锥的体积,求出底面的面积和高,利用三棱锥体积公式即可
(2)存在点N,取CD的中点N,易证平行四边形ABCN为正方形和D1N∥A1B,D1N∥平面A1BC,求三棱锥的体积,求出底面的面积和高,利用三棱锥体积公式即可
解答:
 解:(1)∵四棱柱ABCD-A1B1C1D1侧棱与底面垂直,BC?底面ABCD,且A1A=AB=BC=1
解:(1)∵四棱柱ABCD-A1B1C1D1侧棱与底面垂直,BC?底面ABCD,且A1A=AB=BC=1
∴B1B⊥BC,四边形B1BAA1为正方形,
∴AB1⊥A1B,
∵AB⊥BC,AB∩B1B=B,
∴BC⊥平面B1BAA1,
∵AB1?平面B1BAA1,
∴BC⊥AB1,
∵A1B∩BC=B,
∴AB1⊥平面A1BC,
(2)存在点N,
取CD的中点N,连接AN,AD1,D1N,
∵CD=2,AB=1,
∴CN=
CD=1=AB,
又AB∥CD,
∴四边形ABCN为平行四边形
∵AB⊥BC,AB=BC=1,
∴平行四边形ABCN为正方形,
∴AN∥BC,
∵四棱柱ABCD-A1B1C1D1侧棱与底面垂直,
∴平面B1BAA1∥平面CDD1C1,
∵D1N?平面CDD1C1,A1B?平面B1BAA1,
∴D1N∥A1B,
∵D1N∩AN=N,D1N,AN?平面AND1,A1B∩BC=B,A1B,BC?平面A1BC,
∴平面AND1∥平面A1BC,
∵D1N?平面AND1,
∴D1N∥平面A1BC,
在三棱锥N-AA1C,
∵四棱柱ABCD-A1B1C1D1侧棱与底面垂直,
∴A1A⊥平面ANC,
又平行四边形ABCN为正方形,
∴S△ACN=
×1×1=
,
∵A1A=1,
∴VN-AA1C=
×
×1=
 解:(1)∵四棱柱ABCD-A1B1C1D1侧棱与底面垂直,BC?底面ABCD,且A1A=AB=BC=1
解:(1)∵四棱柱ABCD-A1B1C1D1侧棱与底面垂直,BC?底面ABCD,且A1A=AB=BC=1∴B1B⊥BC,四边形B1BAA1为正方形,
∴AB1⊥A1B,
∵AB⊥BC,AB∩B1B=B,
∴BC⊥平面B1BAA1,
∵AB1?平面B1BAA1,
∴BC⊥AB1,
∵A1B∩BC=B,
∴AB1⊥平面A1BC,
(2)存在点N,
取CD的中点N,连接AN,AD1,D1N,
∵CD=2,AB=1,
∴CN=
| 1 |
| 2 |
又AB∥CD,
∴四边形ABCN为平行四边形
∵AB⊥BC,AB=BC=1,
∴平行四边形ABCN为正方形,
∴AN∥BC,
∵四棱柱ABCD-A1B1C1D1侧棱与底面垂直,
∴平面B1BAA1∥平面CDD1C1,
∵D1N?平面CDD1C1,A1B?平面B1BAA1,
∴D1N∥A1B,
∵D1N∩AN=N,D1N,AN?平面AND1,A1B∩BC=B,A1B,BC?平面A1BC,
∴平面AND1∥平面A1BC,
∵D1N?平面AND1,
∴D1N∥平面A1BC,
在三棱锥N-AA1C,
∵四棱柱ABCD-A1B1C1D1侧棱与底面垂直,
∴A1A⊥平面ANC,
又平行四边形ABCN为正方形,
∴S△ACN=
| 1 |
| 2 |
| 1 |
| 2 |
∵A1A=1,
∴VN-AA1C=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查空间中直线与平面之间的位置关系,是一个非常适合作为高考题目出现的问题,题目包含的知识点比较全面,重点突出.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
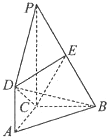 如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.
如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.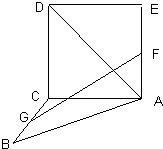 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.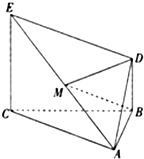 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=2BD,M是EA的中点
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=2BD,M是EA的中点