题目内容
17.设等差数列{an}的公差为6,且a4为a2和a3的等比中项.则a1=-14,数列{an}的前n项和Sn=3n2-17n.分析 运用等比数列的中项的性质,结合等差数列的通项公式,解得首项,再由等差数列的求和公式计算即可得到所求和.
解答 解:由a4为a2和a3的等比中项,可得
a42=a2a3,
即有(a1+18)2=(a1+6)(a1+12),
解方程可得a1=-14,
数列{an}的前n项和Sn=na1+$\frac{1}{2}$n(n-1)d=-14n+$\frac{1}{2}$n(n-1)•6=3n2-17.
故答案为:-14,3n2-17.
点评 本题考查等差数列的通项公式和求和公式的运用,同时考查等比数列的中项的性质,考查运算能力,属于基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
12.当x>1时,关于函数f(x)=x+$\frac{1}{x-1}$,下列叙述正确的是( )
| A. | 函数f(x)有最小值2 | B. | 函数f(x)有最大值2 | C. | 函数f(x)有最小值3 | D. | 函数f(x)有最大值3 |
2.在△ABC中,a=2$\sqrt{3},b=3\sqrt{2},cosC=\frac{1}{3}$,则△ABC的面积为( )
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | $\sqrt{3}$ |
7.在空间直角坐标系中,A(0,0,2),B(2,2,2),在平面xoy中找一点P,使得|PA|+|PB|最小,则点P的坐标为( )
| A. | (0,0,0) | B. | (2,2,0) | C. | (1,1,0) | D. | (0,1,0) |
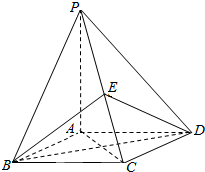 如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.
如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.