题目内容
如图直线MN与⊙O相切于C，AB为直径，∠CAB=40°，则∠MCA的度数为（ ）
| A、50° | B、40° |
| C、60° | D、55° |
考点：弦切角
专题：立体几何
分析：连接OC，由于OC是切线，那么∠OCD=90°，又∠CAB=40°，OA=OC，易求∠ACO=40°，从而可求∠ACM；
解答：
解：连接OC，
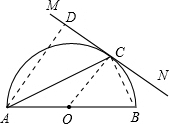
∵MN是⊙O切线，
∴∠OCD=90°，
又∵∠CAB=40°，OA=OC，
∴∠ACO=40°，
∴∠MCA=∠OCD-∠ACO=90°-40°=50°；
故选：A
∵MN是⊙O切线，
∴∠OCD=90°，
又∵∠CAB=40°，OA=OC，
∴∠ACO=40°，
∴∠MCA=∠OCD-∠ACO=90°-40°=50°；
故选：A
点评：本题考查了切线的性质，分析∠MCA，∠ACO与∠CAB的关系是解答的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
某产品每三年降价
，目前价格是640，则9年后此产品的价格是（ ）
| 1 |
| 4 |
| A、270 | B、240 |
| C、210 | D、360 |
“m＜1”是“函数f（x）=x2-x+
m存在零点”的（ ）
| 1 |
| 4 |
| A、充分不必要条件 |
| B、充要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
不等式2x2-4x＞22ax+a对一切实数x都成立，则实数a的取值范围是（ ）
| A、（1，4） |
| B、（-4，-1） |
| C、（-∞，-4）∪（-1，+∞） |
| D、（-∞，1）∪（4，+∞） |
已知5555=8k+m，（k，m∈N*），则整数m可以为（ ）
| A、1 | B、2 | C、6 | D、7 |
P为矩形ABCD所在平面外一点，矩形对角线交点为O，M为PB的中点，给出五个结论：①OM∥PD；②OM∥平面PCD；③OM∥平面PDA；④OM∥平面PBA，⑤OM∥平面PCB．