题目内容
一只昆虫在边长分别为5,12,13的三角形区域内随机爬行,则其到三角形顶点的距离小于2的地方的概率为 .
考点:几何概型
专题:概率与统计
分析:先求出三角形的面积,再求出据三角形的三顶点距离小于等于2的区域为三个扇形,三个扇形的和是半圆,求出半圆的面积,利用几何概型概率公式求出恰在离三个顶点距离都小于2的地方的概率.
解答:
解:昆虫活动的范围是在三角形的内部,三角形的边长为5,12,13,是直角三角形,
∴面积为30, 而“恰在离三个顶点距离都小于2”正好是一个半径为2的半圆,面积为
而“恰在离三个顶点距离都小于2”正好是一个半径为2的半圆,面积为
π×22=4π×
=2π,
∴根据几何概型的概率公式可知其到三角形顶点的距离小于2的地方的概率为
=
.
故答案为:
;
∴面积为30,
 而“恰在离三个顶点距离都小于2”正好是一个半径为2的半圆,面积为
而“恰在离三个顶点距离都小于2”正好是一个半径为2的半圆,面积为| 1 |
| 2 |
| 1 |
| 2 |
∴根据几何概型的概率公式可知其到三角形顶点的距离小于2的地方的概率为
| 2π |
| 30 |
| π |
| 15 |
故答案为:
| π |
| 15 |
点评:本题主要考查几何概型概率公式、三角形的面积公式、圆的面积公式,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
由数字1,2,3,4组成的五位数
中,任意取出一个,满足条件;“对任意的正整数j(1≤j≤5),至少存在另一个正整数k(1≤k≤5,且k≠j),使得aj=ak”的概率为( )
. |
| a1a2a3a4a5 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知函数f(x)=2x+x,g(x)=log3x+x,h(x)=x-
的零点依次为a,b,c,则( )
| 1 | ||
|
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
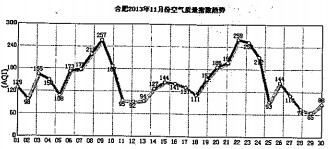 合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图.
合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图.

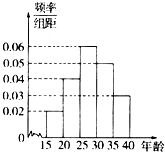 山东省第二十三届运动会将于2014年9月16日在济宁市开幕,为办好省运会,济宁市计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对济宁市15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图及表:
山东省第二十三届运动会将于2014年9月16日在济宁市开幕,为办好省运会,济宁市计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对济宁市15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图及表: